D Exercise solutions

The chapter exercises use the survey design objects and packages provided in the Prerequisites box in the beginning of the chapter. Please ensure they are loaded in the environment before running the exercise solutions. Code chunks to load these are also included below.

library(tidyverse)
library(survey)
library(srvyr)
library(srvyrexploR)
library(broom)
library(prettyunits)
library(gt)
targetpop <- 231592693

anes_adjwgt <- anes_2020 %>%
  mutate(Weight = Weight / sum(Weight) * targetpop)

anes_des <- anes_adjwgt %>%
  as_survey_design(
    weights = Weight,
    strata = Stratum,
    ids = VarUnit,
    nest = TRUE
  )
recs_des <- recs_2020 %>%
  as_survey_rep(
    weights = NWEIGHT,
    repweights = NWEIGHT1:NWEIGHT60,
    type = "JK1",
    scale = 59/60,
    mse = TRUE
  )
inc_series <- ncvs_2021_incident %>%
  mutate(
    series = case_when(V4017 %in% c(1, 8) ~ 1,
                       V4018 %in% c(2, 8) ~ 1,
                       V4019 %in% c(1, 8) ~ 1,
                       TRUE ~ 2
    ),
    n10v4016 = case_when(V4016 %in% c(997, 998) ~ NA_real_,
                         V4016 > 10 ~ 10,
                         TRUE ~ V4016),
    serieswgt = case_when(series == 2 & is.na(n10v4016) ~ 6,
                          series == 2 ~ n10v4016,
                          TRUE ~ 1),
    NEWWGT = WGTVICCY * serieswgt
  )

inc_ind <- inc_series %>%
  filter(V4022 != 1) %>%
  mutate(
    WeapCat = case_when(
      is.na(V4049) ~ NA_character_,
      V4049 == 2 ~ "NoWeap",
      V4049 == 3 ~ "UnkWeapUse",
      V4050 == 3 ~ "Other",
      V4051 == 1 | V4052 == 1 | V4050 == 7 ~ "Firearm",
      V4053 == 1 | V4054 == 1 ~ "Knife",
      TRUE ~ "Other"
    ),
    V4529_num = parse_number(as.character(V4529)),
    ReportPolice = V4399 == 1,
    Property = V4529_num >= 31,
    Violent = V4529_num <= 20,
    Property_ReportPolice = Property & ReportPolice,
    Violent_ReportPolice = Violent & ReportPolice,
    AAST = V4529_num %in% 11:13,
    AAST_NoWeap = AAST & WeapCat == "NoWeap",
    AAST_Firearm = AAST & WeapCat == "Firearm",
    AAST_Knife = AAST & WeapCat == "Knife",
    AAST_Other = AAST & WeapCat == "Other"
  )
inc_hh_sums <-
  inc_ind %>%
  filter(V4529_num > 23) %>% # restrict to household crimes
  group_by(YEARQ, IDHH) %>%
  summarize(WGTVICCY = WGTVICCY[1],
            across(starts_with("Property"), 
                   ~ sum(. * serieswgt),
                   .names = "{.col}"),
            .groups = "drop")

inc_pers_sums <-
  inc_ind %>%
  filter(V4529_num <= 23) %>% # restrict to person crimes
  group_by(YEARQ, IDHH, IDPER) %>%
  summarize(WGTVICCY = WGTVICCY[1],
            across(c(starts_with("Violent"), starts_with("AAST")),
                   ~ sum(. * serieswgt), 
                   .names = "{.col}"),
            .groups = "drop")

hh_z_list <- rep(0, ncol(inc_hh_sums) - 3) %>% as.list() %>%
  setNames(names(inc_hh_sums)[-(1:3)])
pers_z_list <- rep(0, ncol(inc_pers_sums) - 4) %>% as.list() %>%
  setNames(names(inc_pers_sums)[-(1:4)])

hh_vsum <- ncvs_2021_household %>%
  full_join(inc_hh_sums, by = c("YEARQ", "IDHH")) %>%
  replace_na(hh_z_list) %>%
  mutate(ADJINC_WT = if_else(is.na(WGTVICCY), 0, WGTVICCY / WGTHHCY))

pers_vsum <- ncvs_2021_person %>%
  full_join(inc_pers_sums, by = c("YEARQ", "IDHH", "IDPER")) %>%
  replace_na(pers_z_list) %>%
  mutate(ADJINC_WT = if_else(is.na(WGTVICCY), 0, WGTVICCY / WGTPERCY))

hh_vsum_der <- hh_vsum %>%
  mutate(
    Tenure = factor(case_when(V2015 == 1 ~ "Owned", 
                              !is.na(V2015) ~ "Rented"),
                    levels = c("Owned", "Rented")),
    Urbanicity = factor(case_when(V2143 == 1 ~ "Urban",
                                  V2143 == 2 ~ "Suburban",
                                  V2143 == 3 ~ "Rural"),
                        levels = c("Urban", "Suburban", "Rural")),
    SC214A_num = as.numeric(as.character(SC214A)),
    Income = case_when(SC214A_num <= 8 ~ "Less than $25,000",
                       SC214A_num <= 12 ~ "$25,000--49,999",
                       SC214A_num <= 15 ~ "$50,000--99,999",
                       SC214A_num <= 17 ~ "$100,000--199,999",
                       SC214A_num <= 18 ~ "$200,000 or more"),
    Income = fct_reorder(Income, SC214A_num, .na_rm = FALSE),
    PlaceSize = case_match(as.numeric(as.character(V2126B)),
                           0 ~ "Not in a place",
                           13 ~ "Population under 10,000",
                           16 ~ "10,000--49,999",
                           17 ~ "50,000--99,999",
                           18 ~ "100,000--249,999",
                           19 ~ "250,000--499,999",
                           20 ~ "500,000--999,999",
                           c(21, 22, 23) ~ "1,000,000 or more"),
    PlaceSize = fct_reorder(PlaceSize, as.numeric(V2126B)),
    Region = case_match(as.numeric(V2127B),
                        1 ~ "Northeast",
                        2 ~ "Midwest",
                        3 ~ "South",
                        4 ~ "West"),
    Region = fct_reorder(Region, as.numeric(V2127B))
  )
NHOPI <- "Native Hawaiian or Other Pacific Islander"

pers_vsum_der <- pers_vsum %>%
  mutate(
    Sex = factor(case_when(V3018 == 1 ~ "Male",
                           V3018 == 2 ~ "Female")),
    RaceHispOrigin = factor(case_when(V3024 == 1 ~ "Hispanic",
                                      V3023A == 1 ~ "White",
                                      V3023A == 2 ~ "Black",
                                      V3023A == 4 ~ "Asian",
                                      V3023A == 5 ~ NHOPI,
                                      TRUE ~ "Other"),
                            levels = c("White", "Black", "Hispanic", 
                                       "Asian", NHOPI, "Other")),
    V3014_num = as.numeric(as.character(V3014)),
    AgeGroup = case_when(V3014_num <= 17 ~ "12--17",
                         V3014_num <= 24 ~ "18--24",
                         V3014_num <= 34 ~ "25--34",
                         V3014_num <= 49 ~ "35--49",
                         V3014_num <= 64 ~ "50--64",
                         V3014_num <= 90 ~ "65 or older"),
    AgeGroup = fct_reorder(AgeGroup, V3014_num),
    MaritalStatus = factor(case_when(V3015 == 1 ~ "Married",
                                     V3015 == 2 ~ "Widowed",
                                     V3015 == 3 ~ "Divorced",
                                     V3015 == 4 ~ "Separated",
                                     V3015 == 5 ~ "Never married"),
                           levels = c("Never married", "Married", 
                                      "Widowed","Divorced", 
                                      "Separated"))
  ) %>% 
  left_join(hh_vsum_der %>% select(YEARQ, IDHH, 
                                   V2117, V2118, Tenure:Region),
            by = c("YEARQ", "IDHH"))
hh_vsum_slim <- hh_vsum_der %>%
  select(YEARQ:V2118,
         WGTVICCY:ADJINC_WT,
         Tenure,
         Urbanicity,
         Income,
         PlaceSize,
         Region)

pers_vsum_slim <- pers_vsum_der %>%
  select(YEARQ:WGTPERCY, WGTVICCY:ADJINC_WT, Sex:Region)

dummy_records <- hh_vsum_slim %>%
  distinct(V2117, V2118) %>%
  mutate(Dummy = 1,
         WGTVICCY = 1,
         NEWWGT = 1)

inc_analysis <- inc_ind %>%
  mutate(Dummy = 0) %>%
  left_join(select(pers_vsum_slim, YEARQ, IDHH, IDPER, Sex:Region),
            by = c("YEARQ", "IDHH", "IDPER")) %>%
  bind_rows(dummy_records) %>%
  select(YEARQ:IDPER,
         WGTVICCY,
         NEWWGT,
         V4529,
         WeapCat,
         ReportPolice,
         Property:Region)

inc_des <- inc_analysis %>%
  as_survey_design(
    weight = NEWWGT,
    strata = V2117,
    ids = V2118,
    nest = TRUE
  )

hh_des <- hh_vsum_slim %>%
  as_survey_design(
    weight = WGTHHCY,
    strata = V2117,
    ids = V2118,
    nest = TRUE
  )

pers_des <- pers_vsum_slim %>%
  as_survey_design(
    weight = WGTPERCY,
    strata = V2117,
    ids = V2118,
    nest = TRUE
  )

The chapter exercises use the survey design objects and packages provided in the Prerequisites box in the beginning of the chapter. Please ensure they are loaded in the environment before running the exercise solutions.

5 - Descriptive analysis

  1. How many females have a graduate degree? Hint: The variables Gender and Education will be useful.
# Option 1:
femgd_option1 <- anes_des %>%
  filter(Gender == "Female", Education == "Graduate") %>%
  survey_count(name = "n")

femgd_option1
## # A tibble: 1 × 2
##           n    n_se
##       <dbl>   <dbl>
## 1 15072196. 837872.
# Option 2:
femgd_option2 <- anes_des %>%
  filter(Gender == "Female", Education == "Graduate") %>%
  summarize(N = survey_total(), .groups = "drop")

femgd_option2
## # A tibble: 1 × 2
##           N    N_se
##       <dbl>   <dbl>
## 1 15072196. 837872.

Answer: 15,072,196

  1. What percentage of people identify as “Strong Democrat”? Hint: The variable PartyID indicates someone’s party affiliation.
psd <- anes_des %>%
  group_by(PartyID) %>%
  summarize(p = survey_mean()) %>%
  filter(PartyID == "Strong democrat")

psd
## # A tibble: 1 × 3
##   PartyID             p    p_se
##   <fct>           <dbl>   <dbl>
## 1 Strong democrat 0.219 0.00646

Answer: 21.9%

  1. What percentage of people who voted in the 2020 election identify as “Strong Republican”? Hint: The variable VotedPres2020 indicates whether someone voted in 2020.
psr <- anes_des %>%
  filter(VotedPres2020 == "Yes") %>%
  group_by(PartyID) %>%
  summarize(p = survey_mean()) %>%
  filter(PartyID == "Strong republican")

psr
## # A tibble: 1 × 3
##   PartyID               p    p_se
##   <fct>             <dbl>   <dbl>
## 1 Strong republican 0.228 0.00824

Answer: 22.8%

  1. What percentage of people voted in both the 2016 election and the 2020 election? Include the logit confidence interval. Hint: The variable VotedPres2016 indicates whether someone voted in 2016.
pvb <- anes_des %>%
  filter(!is.na(VotedPres2016), !is.na(VotedPres2020)) %>%
  group_by(interact(VotedPres2016, VotedPres2020)) %>%
  summarize(p = survey_prop(var = "ci", method = "logit"), ) %>%
  filter(VotedPres2016 == "Yes", VotedPres2020 == "Yes")

pvb
## # A tibble: 1 × 5
##   VotedPres2016 VotedPres2020     p p_low p_upp
##   <fct>         <fct>         <dbl> <dbl> <dbl>
## 1 Yes           Yes           0.794 0.777 0.810

Answer: 79.4 with confidence interval: (77.7, 81)

  1. What is the design effect for the proportion of people who voted early? Hint: The variable EarlyVote2020 indicates whether someone voted early in 2020.
pdeff <- anes_des %>%
  filter(!is.na(EarlyVote2020)) %>%
  group_by(EarlyVote2020) %>%
  summarize(p = survey_mean(deff = TRUE)) %>%
  filter(EarlyVote2020 == "Yes")

pdeff
## # A tibble: 1 × 4
##   EarlyVote2020     p   p_se p_deff
##   <fct>         <dbl>  <dbl>  <dbl>
## 1 Yes           0.726 0.0247   1.50

Answer: 1.5

  1. What is the median temperature people set their thermostats to at night during the winter? Hint: The variable WinterTempNight indicates the temperature that people set their thermostat to in the winter at night.
med_wintertempnight <- recs_des %>%
  summarize(wtn_med = survey_median(
    x = WinterTempNight,
    na.rm = TRUE
  ))

med_wintertempnight
## # A tibble: 1 × 2
##   wtn_med wtn_med_se
##     <dbl>      <dbl>
## 1      68      0.250

Answer: 68

  1. People sometimes set their temperature differently over different seasons and during the day. What median temperatures do people set their thermostat to in the summer and winter, both during the day and at night? Include confidence intervals. Hint: Use the variables WinterTempDay, WinterTempNight, SummerTempDay, and SummerTempNight.
# Option 1

med_temps <- recs_des %>%
  summarize(
    across(c(WinterTempDay, WinterTempNight, SummerTempDay, SummerTempNight), ~ survey_median(.x, na.rm = TRUE))
  )

med_temps
## # A tibble: 1 × 8
##   WinterTempDay WinterTempDay_se WinterTempNight WinterTempNight_se
##           <dbl>            <dbl>           <dbl>              <dbl>
## 1            70            0.250              68              0.250
## # ℹ 4 more variables: SummerTempDay <dbl>, SummerTempDay_se <dbl>,
## #   SummerTempNight <dbl>, SummerTempNight_se <dbl>
# Alternatively, could use `survey_quantile()` as shown below for WinterTempNight:

quant_temps <- recs_des %>%
  summarize(
    across(c(WinterTempDay, WinterTempNight, SummerTempDay, SummerTempNight), ~ survey_quantile(.x, quantiles = 0.5, na.rm = TRUE))
  )

quant_temps
## # A tibble: 1 × 8
##   WinterTempDay_q50 WinterTempDay_q50_se WinterTempNight_q50
##               <dbl>                <dbl>               <dbl>
## 1                70                0.250                  68
## # ℹ 5 more variables: WinterTempNight_q50_se <dbl>,
## #   SummerTempDay_q50 <dbl>, SummerTempDay_q50_se <dbl>,
## #   SummerTempNight_q50 <dbl>, SummerTempNight_q50_se <dbl>

Answer: - Winter during the day: 70 - Winter during the night: 68 - Summer during the day: 72 - Summer during the night: 72

  1. What is the correlation between the temperature that people set their temperature at during the night and during the day in the summer?
corr_summer_temp <- recs_des %>%
  summarize(summer_corr = survey_corr(SummerTempNight, SummerTempDay,
    na.rm = TRUE
  ))

corr_summer_temp
## # A tibble: 1 × 2
##   summer_corr summer_corr_se
##         <dbl>          <dbl>
## 1       0.806        0.00806

Answer: 0.806

  1. What is the 1st, 2nd, and 3rd quartile of the amount of money spent on energy by Building America (BA) climate zone? Hint: TOTALDOL indicates the total amount spent on all fuel, and ClimateRegion_BA indicates the BA climate zones.
quant_baenergyexp <- recs_des %>%
  group_by(ClimateRegion_BA) %>%
  summarize(dol_quant = survey_quantile(
    TOTALDOL,
    quantiles = c(0.25, 0.5, 0.75),
    vartype = "se",
    na.rm = TRUE
  ))

quant_baenergyexp
## # A tibble: 8 × 7
##   ClimateRegion_BA dol_quant_q25 dol_quant_q50 dol_quant_q75
##   <fct>                    <dbl>         <dbl>         <dbl>
## 1 Mixed-Dry                1091.         1541.         2139.
## 2 Mixed-Humid              1317.         1840.         2462.
## 3 Hot-Humid                1094.         1622.         2233.
## 4 Hot-Dry                   926.         1513.         2223.
## 5 Very-Cold                1195.         1986.         2955.
## 6 Cold                     1213.         1756.         2422.
## 7 Marine                    938.         1380.         1987.
## 8 Subarctic                2404.         3535.         5219.
## # ℹ 3 more variables: dol_quant_q25_se <dbl>, dol_quant_q50_se <dbl>,
## #   dol_quant_q75_se <dbl>

Answer:

Quartile summary of energy expenditure by BA Climate Zone
Q1 Q2 Q3
Mixed-Dry $1,091 $1,541 $2,139
Mixed-Humid $1,317 $1,840 $2,462
Hot-Humid $1,094 $1,622 $2,233
Hot-Dry $926 $1,513 $2,223
Very-Cold $1,195 $1,986 $2,955
Cold $1,213 $1,756 $2,422
Marine $938 $1,380 $1,987
Subarctic $2,404 $3,535 $5,219

6 - Statistical testing

  1. Using the RECS data, do more than 50% of U.S. households use A/C (ACUsed)?
ttest_solution1 <- recs_des %>%
  svyttest(
    design = .,
    formula = ((ACUsed == TRUE) - 0.5) ~ 0,
    na.rm = TRUE,
    alternative = "greater"
  ) %>%
  tidy()

ttest_solution1
## # A tibble: 1 × 8
##   estimate statistic  p.value parameter conf.low conf.high method       
##      <dbl>     <dbl>    <dbl>     <dbl>    <dbl>     <dbl> <chr>        
## 1    0.387      126. 1.73e-72        58    0.380     0.393 Design-based…
## # ℹ 1 more variable: alternative <chr>

Answer: 88.7% of households use air conditioning which is significantly different from 50% (p<0.0001) so there is strong evidence that more than 50% of households use air-conditioning.

  1. Using the RECS data, does the average temperature that U.S. households set their thermostats to differ between the day and night in the winter (WinterTempDay and WinterTempNight)?
ttest_solution2 <- recs_des %>%
  svyttest(
    design = .,
    formula = WinterTempDay - WinterTempNight ~ 0,
    na.rm = TRUE
  ) %>%
  tidy()

ttest_solution2
## # A tibble: 1 × 8
##   estimate statistic  p.value parameter conf.low conf.high method       
##      <dbl>     <dbl>    <dbl>     <dbl>    <dbl>     <dbl> <chr>        
## 1     1.67      45.9 2.82e-47        58     1.59      1.74 Design-based…
## # ℹ 1 more variable: alternative <chr>

Answer: The average temperature difference between night and day during the winter for thermostat settings is 1.67 which is significantly different from 0 (p<0.0001) so there is strong evidence that the temperature setting is different between night and daytime during the winter.

  1. Using the ANES data, does the average age (Age) of those who voted for Joseph Biden in 2020 (VotedPres2020_selection) differ from those who voted for another candidate?
ttest_solution3 <- anes_des %>%
  filter(!is.na(VotedPres2020_selection)) %>%
  svyttest(
    design = .,
    formula = Age ~ VotedPres2020_selection == "Biden",
    na.rm = TRUE
  ) %>%
  tidy()

ttest_solution3
## # A tibble: 1 × 8
##   estimate statistic     p.value parameter conf.low conf.high method    
##      <dbl>     <dbl>       <dbl>     <dbl>    <dbl>     <dbl> <chr>     
## 1    -3.60     -5.97 0.000000244        50    -4.81     -2.39 Design-ba…
## # ℹ 1 more variable: alternative <chr>

On average, those who voted for Joseph Biden in 2020 were -3.6 years younger than voters for other candidates and this is significantly different (p <0.0001).

  1. If we wanted to determine if the political party affiliation differed for males and females, what test would we use?
  1. Goodness-of-fit test (svygofchisq())
  2. Test of independence (svychisq())
  3. Test of homogeneity (svychisq())

Answer: c. Test of homogeneity (svychisq())

  1. In the RECS data, is there a relationship between the type of housing unit (HousingUnitType) and the year the house was built (YearMade)?
chisq_solution2 <- recs_des %>%
  svychisq(
    formula = ~ HousingUnitType + YearMade,
    design = .,
    statistic = "Wald",
    na.rm = TRUE
  )

chisq_solution2 %>% tidy()
## Multiple parameters; naming those columns ndf, ddf
## # A tibble: 1 × 5
##     ndf   ddf statistic  p.value method                               
##   <dbl> <dbl>     <dbl>    <dbl> <chr>                                
## 1    32    59      67.9 5.54e-36 Design-based Wald test of association

Answer: There is strong evidence (p<0.0001) that there is a relationship between type of housing unit and the year the house was built.

  1. In the ANES data, is there a difference in the distribution of gender (Gender) across early voting status in 2020 (EarlyVote2020)?
chisq_solution3 <- anes_des %>%
  svychisq(
    formula = ~ Gender + EarlyVote2020,
    design = .,
    statistic = "F",
    na.rm = TRUE
  ) %>%
  tidy()
## Multiple parameters; naming those columns ndf, ddf
chisq_solution3
## # A tibble: 1 × 5
##     ndf   ddf statistic p.value method                               
##   <dbl> <dbl>     <dbl>   <dbl> <chr>                                
## 1     1    51      4.53  0.0381 Pearson's X^2: Rao & Scott adjustment

Answer: There is strong evidence that there is a difference in the gender distribution of gender by early voting status (p=0.0381).

7 - Modeling

  1. The type of housing unit may have an impact on energy expenses. Is there any relationship between housing unit type (HousingUnitType) and total energy expenditure (TOTALDOL)? First, find the average energy expenditure by housing unit type as a descriptive analysis and then do the test. The reference level in the comparison should be the housing unit type that is most common.
expense_by_hut <- recs_des %>%
  group_by(HousingUnitType) %>%
  summarize(
    Expense = survey_mean(TOTALDOL, na.rm = TRUE),
    HUs = survey_total()
  ) %>%
  arrange(desc(HUs))

expense_by_hut
## # A tibble: 5 × 5
##   HousingUnitType            Expense Expense_se       HUs       HUs_se
##   <fct>                        <dbl>      <dbl>     <dbl>        <dbl>
## 1 Single-family detached       2205.       9.36 77067692. 0.00000277  
## 2 Apartment: 5 or more units   1108.      13.7  22835862. 0.000000226 
## 3 Apartment: 2-4 Units         1407.      24.2   9341795. 0.119       
## 4 Single-family attached       1653.      22.3   7451177. 0.114       
## 5 Mobile home                  1773.      26.2   6832499. 0.0000000927
exp_unit_out <- recs_des %>%
  mutate(HousingUnitType = fct_infreq(HousingUnitType, NWEIGHT)) %>%
  svyglm(
    design = .,
    formula = TOTALDOL ~ HousingUnitType,
    na.action = na.omit
  )

tidy(exp_unit_out)
## # A tibble: 5 × 5
##   term                             estimate std.error statistic  p.value
##   <chr>                               <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)                         2205.      9.36     236.  2.53e-84
## 2 HousingUnitTypeApartment: 5 or …   -1097.     16.5      -66.3 3.52e-54
## 3 HousingUnitTypeApartment: 2-4 U…    -798.     28.0      -28.5 1.37e-34
## 4 HousingUnitTypeSingle-family at…    -551.     25.0      -22.1 5.28e-29
## 5 HousingUnitTypeMobile home          -431.     27.4      -15.7 5.36e-22

Answer: The reference level should be Single-family detached. All p-values are very small indicating there is a significant relationship between housing unit type and total energy expenditure.

  1. Does temperature play a role in electricity expenditure? Cooling degree days are a measure of how hot a place is. CDD65 for a given day indicates the number of degrees Fahrenheit warmer than 65°F (18.3°C) it is in a location. On a day that averages 65°F and below, CDD65=0. While a day that averages 85°F (29.4°C) would have CDD65=20 because it is 20 degrees Fahrenheit warmer (U.S. Energy Information Administration 2023d). For each day in the year, this is summed to give an indicator of how hot the place is throughout the year. Similarly, HDD65 indicates the days colder than 65°F. Can energy expenditure be predicted using these temperature indicators along with square footage? Is there a significant relationship? Include main effects and two-way interactions.
temps_sqft_exp <- recs_des %>%
  svyglm(
    design = .,
    formula = DOLLAREL ~ (TOTSQFT_EN + CDD65 + HDD65)^2,
    na.action = na.omit
  )

tidy(temps_sqft_exp) %>%
  mutate(p.value = pretty_p_value(p.value) %>% str_pad(7))
## # A tibble: 7 × 5
##   term                 estimate   std.error statistic p.value  
##   <chr>                   <dbl>       <dbl>     <dbl> <chr>    
## 1 (Intercept)      741.         70.5           10.5   "<0.0001"
## 2 TOTSQFT_EN         0.272       0.0471         5.77  "<0.0001"
## 3 CDD65              0.0293      0.0227         1.29  " 0.2024"
## 4 HDD65             -0.00111     0.0104        -0.107 " 0.9149"
## 5 TOTSQFT_EN:CDD65   0.0000459   0.0000154      2.97  " 0.0044"
## 6 TOTSQFT_EN:HDD65  -0.00000840  0.00000633    -1.33  " 0.1902"
## 7 CDD65:HDD65        0.00000533  0.00000355     1.50  " 0.1390"

Answer: There is a significant interaction between square footage and cooling degree days in the model and the square footage is a significant predictor of eletricity expenditure.

  1. Continuing with our results from Exercise 2, create a plot between the actual and predicted expenditures and a residual plot for the predicted expenditures.

Answer:

temps_sqft_exp_fit <- temps_sqft_exp %>%
  augment() %>%
  mutate(
    .se.fit = sqrt(attr(.fitted, "var")),
    # extract the variance of the fitted value
    .fitted = as.numeric(.fitted)
  )
temps_sqft_exp_fit %>%
  ggplot(aes(x = DOLLAREL, y = .fitted)) +
  geom_point() +
  geom_abline(
    intercept = 0,
    slope = 1,
    color = "red"
  ) +
  xlab("Actual expenditures") +
  ylab("Predicted expenditures") +
  theme_minimal()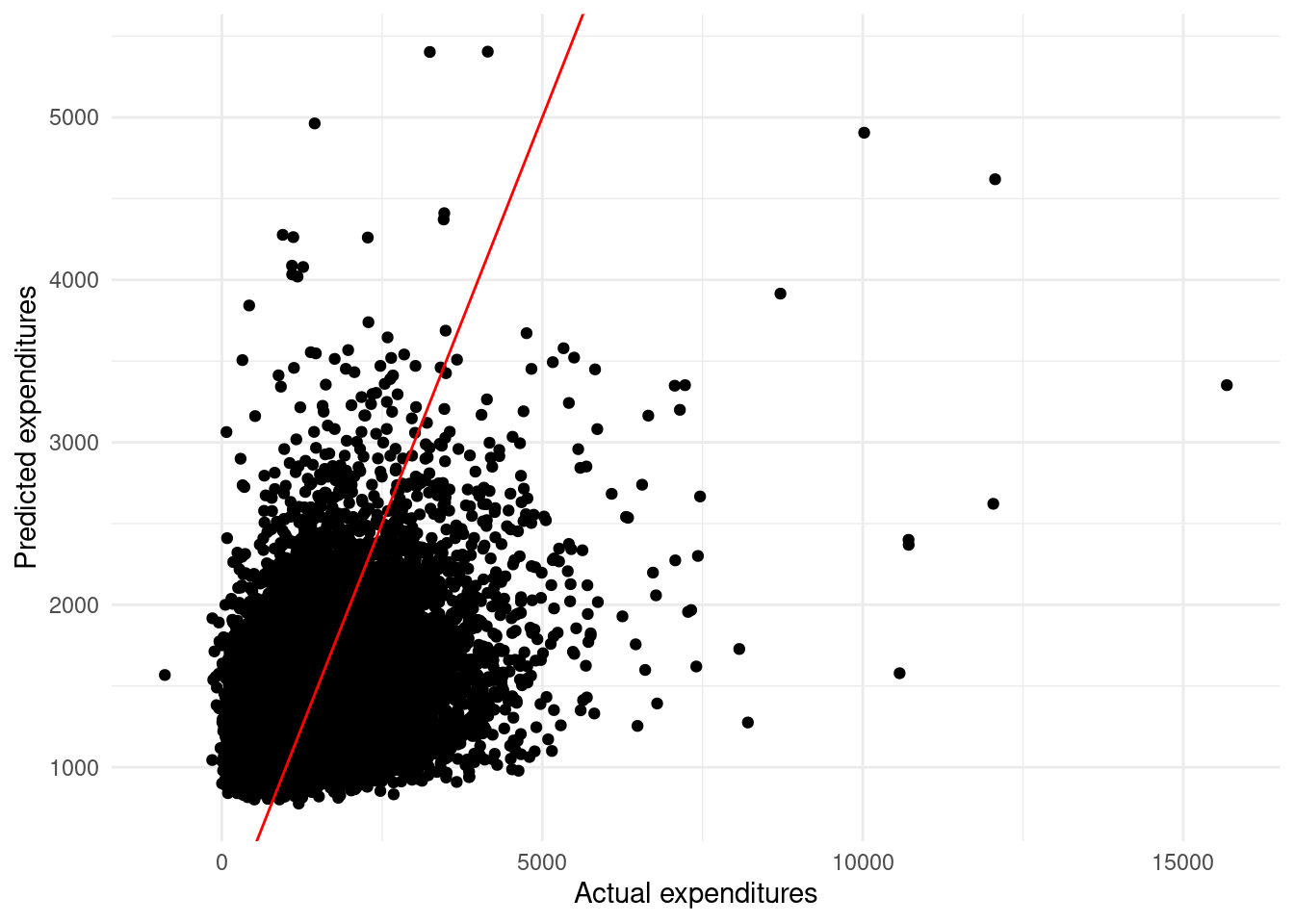
Actual and predicted electricity expenditures

FIGURE D.1: Actual and predicted electricity expenditures 

temps_sqft_exp_fit %>%
  ggplot(aes(x = .fitted, y = .resid)) +
  geom_point() +
  geom_hline(yintercept = 0, color = "red") +
  xlab("Predicted expenditure") +
  ylab("Residual value of expenditure") +
  theme_minimal()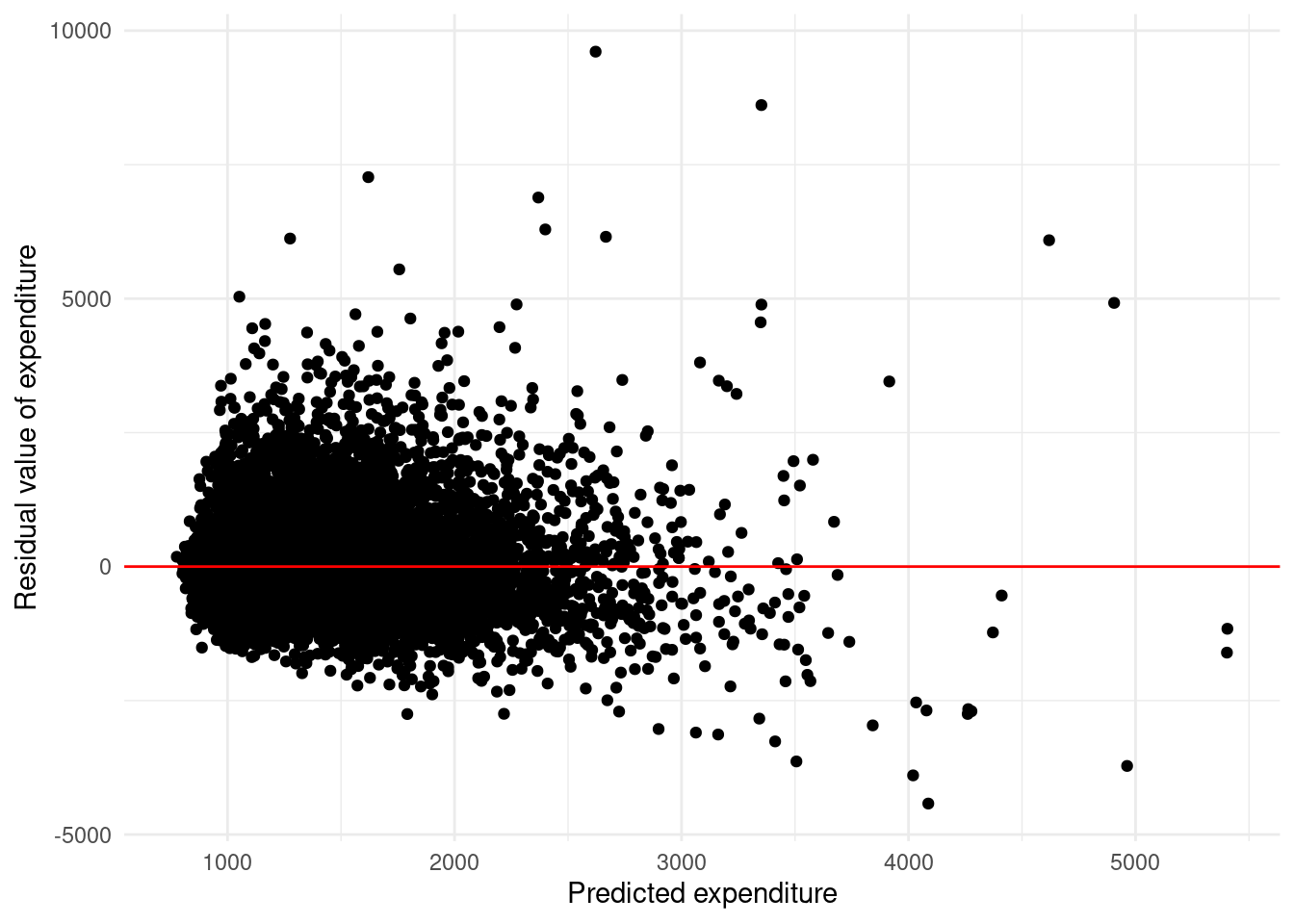
Residual plot of electric cost model with covariates TOTSQFT_EN, CDD65, and HDD65

FIGURE D.2: Residual plot of electric cost model with covariates TOTSQFT_EN, CDD65, and HDD65

  1. Early voting expanded in 2020 (Sprunt 2020). Build a logistic model predicting early voting in 2020 (EarlyVote2020) using age (Age), education (Education), and party identification (PartyID). Include two-way interactions.

Answer:

earlyvote_mod <- anes_des %>%
  filter(!is.na(EarlyVote2020)) %>%
  svyglm(
    design = .,
    formula = EarlyVote2020 ~ (Age + Education + PartyID)^2,
    family = quasibinomial
  )

tidy(earlyvote_mod) %>% print(n = 50)
## # A tibble: 46 × 5
##    term                             estimate std.error statistic p.value
##    <chr>                               <dbl>     <dbl>     <dbl>   <dbl>
##  1 (Intercept)                       3.28e-1    3.86      0.0848  0.940 
##  2 Age                              -2.20e-2    0.0579   -0.379   0.741 
##  3 EducationHigh school             -2.56e+0    3.89     -0.658   0.578 
##  4 EducationPost HS                 -3.27e+0    3.97     -0.823   0.497 
##  5 EducationBachelor's              -3.29e+0    3.91     -0.842   0.489 
##  6 EducationGraduate                -1.36e+0    3.91     -0.349   0.761 
##  7 PartyIDNot very strong democrat   2.00e+0    3.30      0.605   0.607 
##  8 PartyIDIndependent-democrat       3.38e+0    2.60      1.30    0.323 
##  9 PartyIDIndependent                5.22e+0    2.25      2.32    0.146 
## 10 PartyIDIndependent-republican    -1.95e+1    2.42     -8.09    0.0149
## 11 PartyIDNot very strong republic… -1.33e+1    3.24     -4.10    0.0546
## 12 PartyIDStrong republican          3.13e+0    2.18      1.44    0.287 
## 13 Age:EducationHigh school          4.72e-2    0.0592    0.796   0.509 
## 14 Age:EducationPost HS              5.25e-2    0.0588    0.892   0.467 
## 15 Age:EducationBachelor's           4.76e-2    0.0600    0.793   0.511 
## 16 Age:EducationGraduate             8.65e-3    0.0578    0.150   0.895 
## 17 Age:PartyIDNot very strong demo… -2.28e-2    0.0497   -0.459   0.691 
## 18 Age:PartyIDIndependent-democrat  -7.03e-2    0.0285   -2.46    0.133 
## 19 Age:PartyIDIndependent           -8.00e-2    0.0302   -2.65    0.118 
## 20 Age:PartyIDIndependent-republic…  6.72e-2    0.0378    1.78    0.217 
## 21 Age:PartyIDNot very strong repu… -3.07e-2    0.0420   -0.732   0.540 
## 22 Age:PartyIDStrong republican     -3.84e-2    0.0180   -2.14    0.166 
## 23 EducationHigh school:PartyIDNot… -1.24e+0    2.22     -0.557   0.633 
## 24 EducationPost HS:PartyIDNot ver… -8.95e-1    2.16     -0.413   0.719 
## 25 EducationBachelor's:PartyIDNot … -1.21e+0    2.29     -0.528   0.650 
## 26 EducationGraduate:PartyIDNot ve… -1.90e+0    2.25     -0.844   0.487 
## 27 EducationHigh school:PartyIDInd…  7.84e-1    2.50      0.314   0.783 
## 28 EducationPost HS:PartyIDIndepen…  4.04e-1    2.31      0.175   0.877 
## 29 EducationBachelor's:PartyIDInde…  5.00e-1    2.60      0.193   0.865 
## 30 EducationGraduate:PartyIDIndepe… -1.48e+1    2.47     -5.99    0.0268
## 31 EducationHigh school:PartyIDInd… -6.32e-1    1.72     -0.368   0.748 
## 32 EducationPost HS:PartyIDIndepen… -9.27e-2    1.63     -0.0568  0.960 
## 33 EducationBachelor's:PartyIDInde… -2.62e-1    2.13     -0.123   0.913 
## 34 EducationGraduate:PartyIDIndepe… -1.42e+1    1.75     -8.12    0.0148
## 35 EducationHigh school:PartyIDInd…  1.55e+1    2.56      6.05    0.0262
## 36 EducationPost HS:PartyIDIndepen…  1.48e+1    2.77      5.34    0.0333
## 37 EducationBachelor's:PartyIDInde…  1.77e+1    2.32      7.64    0.0167
## 38 EducationGraduate:PartyIDIndepe…  1.65e+1    2.33      7.10    0.0193
## 39 EducationHigh school:PartyIDNot…  1.59e+1    2.02      7.88    0.0157
## 40 EducationPost HS:PartyIDNot ver…  1.62e+1    1.69      9.54    0.0108
## 41 EducationBachelor's:PartyIDNot …  1.58e+1    1.93      8.18    0.0146
## 42 EducationGraduate:PartyIDNot ve…  1.54e+1    1.72      8.95    0.0123
## 43 EducationHigh school:PartyIDStr… -2.06e+0    1.88     -1.10    0.387 
## 44 EducationPost HS:PartyIDStrong …  9.17e-2    2.01      0.0456  0.968 
## 45 EducationBachelor's:PartyIDStro…  6.87e-2    2.06      0.0333  0.976 
## 46 EducationGraduate:PartyIDStrong… -8.53e-1    1.81     -0.471   0.684
  1. Continuing from Exercise 4, predict the probability of early voting for two people. Both are 28 years old and have a graduate degree; however, one person is a strong Democrat, and the other is a strong Republican.
add_vote_dat <- anes_2020 %>%
  select(EarlyVote2020, Age, Education, PartyID) %>%
  rbind(tibble(
    EarlyVote2020 = NA,
    Age = 28,
    Education = "Graduate",
    PartyID = c("Strong democrat", "Strong republican")
  )) %>%
  tail(2)

log_ex_2_out <- earlyvote_mod %>%
  augment(newdata = add_vote_dat, type.predict = "response") %>%
  mutate(
    .se.fit = sqrt(attr(.fitted, "var")),
    # extract the variance of the fitted value
    .fitted = as.numeric(.fitted)
  )

log_ex_2_out
## # A tibble: 2 × 6
##   EarlyVote2020   Age Education PartyID           .fitted .se.fit
##   <fct>         <dbl> <fct>     <fct>               <dbl>   <dbl>
## 1 <NA>             28 Graduate  Strong democrat     0.197   0.150
## 2 <NA>             28 Graduate  Strong republican   0.450   0.244

Answer: We predict that the 28 year old with a graduate degree who identifies as a strong democrat will vote early 19.7% of the time while a person who is otherwise similar but is a strong replican will vote early 45% of the time

10 - Specifying sample designs and replicate weights in {srvyr}

  1. The National Health Interview Survey (NHIS) is an annual household survey conducted by the National Center for Health Statistics (NCHS). The NHIS includes a wide variety of health topics for adults including health status and conditions, functioning and disability, health care access and health service utilization, health-related behaviors, health promotion, mental health, barriers to receiving care, and community engagement. Like many national in-person surveys, the sampling design is a stratified clustered design with details included in the Survey Description (National Center for Health Statistics 2023). The Survey Description provides information on setting up syntax in SUDAAN, Stata, SPSS, SAS, and R ({survey} package implementation). We have imported the data and the variable containing the data as: nhis_adult_data. How would we specify the design using either as_survey_design() or as_survey_rep()?

Answer:

nhis_adult_des <- nhis_adult_data %>%
  as_survey_design(
    ids = PPSU,
    strata = PSTRAT,
    nest = TRUE,
    weights = WTFA_A
  )
  1. The General Social Survey (GSS) is a survey that has been administered since 1972 on social, behavioral, and attitudinal topics. The 2016-2020 GSS Panel codebook provides examples of setting up syntax in SAS and Stata but not R (Davern et al. 2021). We have imported the data and the variable containing the data as: gss_data. How would we specify the design in R using either as_survey_design() or as_survey_rep()?

Answer:

gss_des <- gss_data %>%
  as_survey_design(
    ids = VPSU_2,
    strata = VSTRAT_2,
    weights = WTSSNR_2
  )

13 - National Crime Victimization Survey Vignette

  1. What proportion of completed motor vehicle thefts are not reported to the police? Hint: Use the codebook to look at the definition of Type of Crime (V4529).
ans1 <- inc_des %>%
  filter(str_detect(V4529, "40|41")) %>%
  summarize(Pct = survey_mean(!ReportPolice, na.rm = TRUE) * 100)

Answer: It is estimated that 23.1% of motor vehicle thefts are not reported to the police.

  1. How many violent crimes occur in each region?

Answer:

inc_des %>%
  filter(Violent) %>%
  survey_count(Region) %>%
  select(-n_se) %>%
  gt(rowname_col = "Region") %>%
  fmt_integer() %>%
  cols_label(
    n = "Violent victimizations",
  ) %>%
  tab_header("Estimated number of violent crimes by region")
Estimated number of violent crimes by region
Violent victimizations
Northeast 698,406
Midwest 1,144,407
South 1,394,214
West 1,361,278
  1. What is the property victimization rate among each income level?

Answer:

hh_des %>%
  filter(!is.na(Income)) %>%
  group_by(Income) %>%
  summarize(Property_Rate = survey_mean(Property * ADJINC_WT * 1000,
    na.rm = TRUE
  )) %>%
  gt(rowname_col = "Income") %>%
  cols_label(
    Property_Rate = "Rate",
    Property_Rate_se = "Standard Error"
  ) %>%
  fmt_number(decimals = 1) %>%
  tab_header("Estimated property victimization rate by income level")
Estimated property victimization rate by income level
Rate Standard Error
Less than $25,000 110.6 5.0
$25,000--49,999 89.5 3.4
$50,000--99,999 87.8 3.3
$100,000--199,999 76.5 3.5
$200,000 or more 91.8 5.7
  1. What is the difference between the violent victimization rate between males and females? Is it statistically different?
vr_gender <- pers_des %>%
  group_by(Sex) %>%
  summarize(
    Violent_rate = survey_mean(Violent * ADJINC_WT * 1000, na.rm = TRUE)
  )

vr_gender_test <- pers_des %>%
  mutate(
    Violent_Adj = Violent * ADJINC_WT * 1000
  ) %>%
  svyttest(
    formula = Violent_Adj ~ Sex,
    design = .,
    na.rm = TRUE
  ) %>%
  broom::tidy()
## Warning in summary.glm(g): observations with zero weight not used for
## calculating dispersion
## Warning in summary.glm(glm.object): observations with zero weight not
## used for calculating dispersion

Answer: The difference between male and female victimization rate is estimated as 1.9 victimizations/1,000 people and is not significantly different (p-value=0.1560)

14 - AmericasBarometer Vignette

  1. Calculate the percentage of households with broadband internet and those with any internet at home, including from a phone or tablet in Latin America and the Caribbean. Hint: if there are countries with 0% internet usage, try filtering by something first. Answer:
int_ests <-
  ambarom_des %>%
  filter(!is.na(Internet) | !is.na(BroadbandInternet)) %>%
  group_by(Country) %>%
  summarize(
    p_broadband = survey_mean(BroadbandInternet, na.rm = TRUE) * 100,
    p_internet = survey_mean(Internet, na.rm = TRUE) * 100
  )

int_ests %>%
  gt(rowname_col = "Country") %>%
  fmt_number(decimals = 1) %>%
  tab_spanner(
    label = "Broadband at home",
    columns = c(p_broadband, p_broadband_se)
  ) %>%
  tab_spanner(
    label = "Internet at home",
    columns = c(p_internet, p_internet_se)
  ) %>%
  cols_label(
    p_broadband = "Percent",
    p_internet = "Percent",
    p_broadband_se = "S.E.",
    p_internet_se = "S.E.",
  )
Broadband at home Internet at home
Percent S.E. Percent S.E.
Argentina 62.3 1.1 86.2 0.9
Bolivia 41.4 1.0 77.2 1.0
Brazil 68.3 1.2 88.9 0.9
Chile 63.1 1.1 93.5 0.5
Colombia 45.7 1.2 68.7 1.1
Costa Rica 49.6 1.1 84.4 0.8
Dominican Republic 37.1 1.0 73.7 1.0
Ecuador 59.7 1.1 79.9 0.9
El Salvador 30.2 0.9 63.9 1.0
Guatemala 33.4 1.0 61.5 1.1
Guyana 63.7 1.1 86.8 0.8
Haiti 11.8 0.8 58.5 1.2
Honduras 28.2 1.0 60.7 1.1
Jamaica 64.2 1.0 91.5 0.6
Mexico 44.9 1.1 70.9 1.0
Nicaragua 39.1 1.1 76.3 1.1
Panama 43.4 1.0 73.1 1.0
Paraguay 33.3 1.0 72.9 1.0
Peru 42.4 1.1 71.1 1.1
Uruguay 62.7 1.1 90.6 0.7
  1. Create a faceted map showing both broadband internet and any internet usage.

Answer:

library(sf)
library(rnaturalearth)
library(ggpattern)
internet_sf <- country_shape_upd %>%
  full_join(select(int_ests, p = p_internet, geounit = Country), by = "geounit") %>%
  mutate(Type = "Internet")
broadband_sf <- country_shape_upd %>%
  full_join(select(int_ests, p = p_broadband, geounit = Country), by = "geounit") %>%
  mutate(Type = "Broadband")
b_int_sf <- internet_sf %>%
  bind_rows(broadband_sf) %>%
  filter(region_wb == "Latin America & Caribbean")

b_int_sf %>%
  ggplot(aes(fill = p),
    color = "darkgray"
  ) +
  geom_sf() +
  facet_wrap(~Type) +
  scale_fill_gradientn(
    guide = "colorbar",
    name = "Percent",
    labels = scales::comma,
    colors = c("#BFD7EA", "#087E8B", "#0B3954"),
    na.value = NA
  ) +
  geom_sf_pattern(
    data = filter(b_int_sf, is.na(p)),
    pattern = "crosshatch",
    pattern_fill = "lightgray",
    pattern_color = "lightgray",
    fill = NA,
    color = "darkgray"
  ) +
  theme_minimal()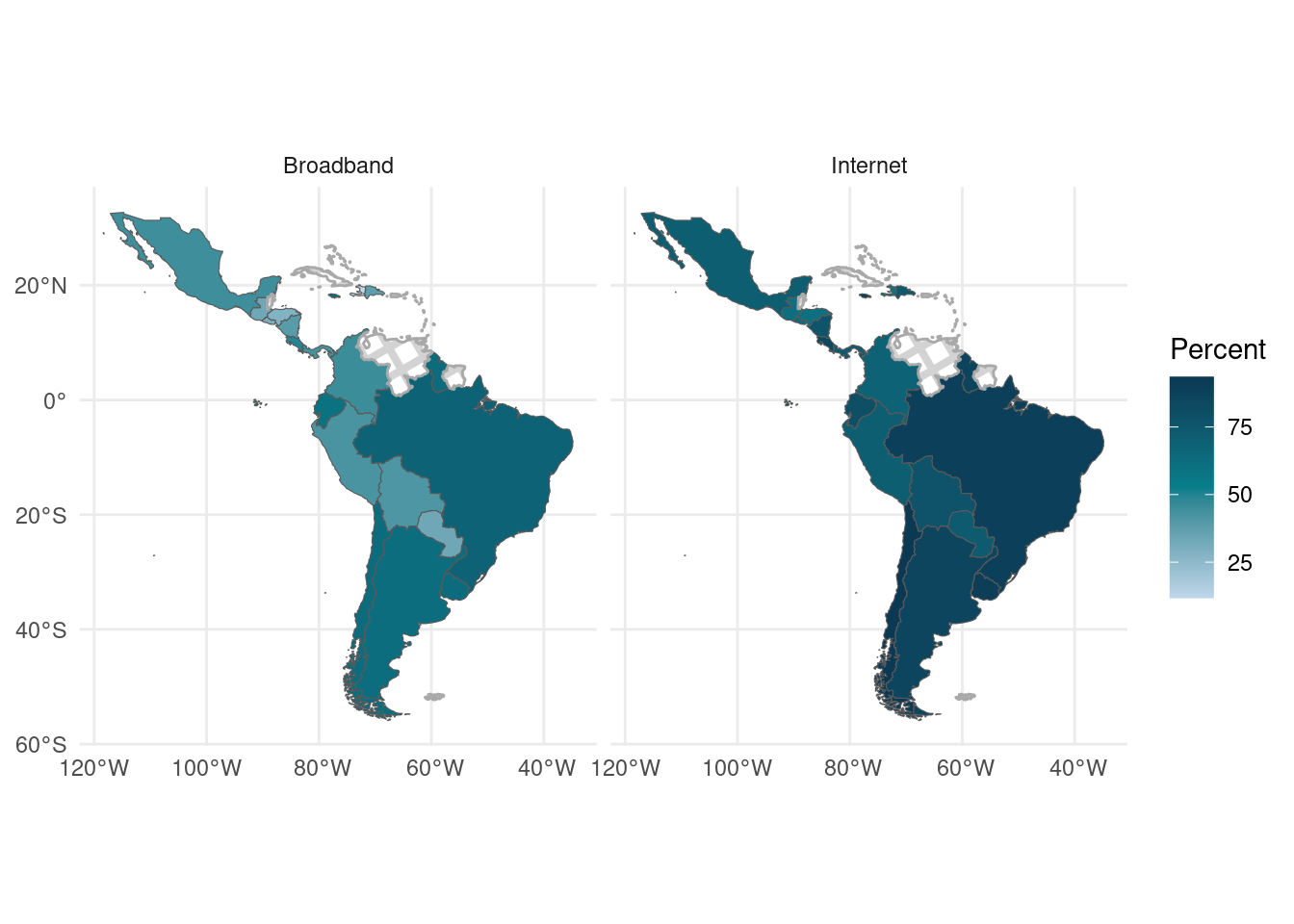
Percent of broadband internet and any internet usage, Central and South America

FIGURE D.3: Percent of broadband internet and any internet usage, Central and South America

References

Davern, Michael, Rene Bautista, Jeremy Freese, Stephen L. Morgan, and Tom W. Smith. 2021. “General Social Survey 2016-2020 Panel Codebook.” Edited by Chicago NORC. https://gss.norc.org/Documents/codebook/2016-2020%20GSS%20Panel%20Codebook%20-%20R1a.pdf.
National Center for Health Statistics. 2023. “National Health Interview Survey, 2022 survey description.” https://ftp.cdc.gov/pub/Health_Statistics/NCHS/Dataset_Documentation/NHIS/2022/srvydesc-508.pdf.
Sprunt, Barbara. 2020. “93 Million and Counting: Americans Are Shattering Early Voting Records.” National Public Radio.
———. 2023d. “Units and Calculators Explained: Degree Days.” https://www.eia.gov/energyexplained/units-and-calculators/degree-days.php.