Chapter 6 Statistical testing

Prerequisites

For this chapter, load the following packages:

library(tidyverse)
library(survey)
library(srvyr)
library(srvyrexploR)
library(broom)
library(gt)
library(prettyunits)

We are using data from ANES and RECS described in Chapter 4. As a reminder, here is the code to create the design objects for each to use throughout this chapter. For ANES, we need to adjust the weight so it sums to the population instead of the sample (see the ANES documentation and Chapter 4 for more information).

targetpop <- 231592693

anes_adjwgt <- anes_2020 %>%
  mutate(Weight = Weight / sum(Weight) * targetpop)

anes_des <- anes_adjwgt %>%
  as_survey_design(
    weights = Weight,
    strata = Stratum,
    ids = VarUnit,
    nest = TRUE
  )

For RECS, details are included in the RECS documentation and Chapters 4 and 10.

recs_des <- recs_2020 %>%
  as_survey_rep(
    weights = NWEIGHT,
    repweights = NWEIGHT1:NWEIGHT60,
    type = "JK1",
    scale = 59 / 60,
    mse = TRUE
  )

6.1 Introduction

When analyzing survey results, the point estimates described in Chapter 5 help us understand the data at a high level. Still, we often want to make comparisons between different groups. These comparisons are calculated through statistical testing.

The general idea of statistical testing is the same for data obtained through surveys and data obtained through other methods, where we compare the point estimates and uncertainty estimates of each statistic to see if statistically significant differences exist. However, statistical testing for complex surveys involves additional considerations due to the need to account for the sampling design in order to obtain accurate uncertainty estimates.

Statistical testing, also called hypothesis testing, involves declaring a null and alternative hypothesis. A null hypothesis is denoted as \(H_0\) and the alternative hypothesis is denoted as \(H_A\). The null hypothesis is the default assumption in that there are no differences in the data, or that the data are operating under “standard” behaviors. On the other hand, the alternative hypothesis is the break from the “standard,” and we are trying to determine if the data support this alternative hypothesis.

Let’s review an example outside of survey data. If we are flipping a coin, a null hypothesis would be that the coin is fair and that each side has an equal chance of being flipped. In other words, the probability of the coin landing on each side is 1/2, whereas an alternative hypothesis could be that the coin is unfair and that one side has a higher probability of being flipped (e.g., a probability of 1/4 to get heads but a probability of 3/4 to get tails). We write this set of hypotheses as:

• \(H_0: \rho_{heads} = \rho_{tails}\), where \(\rho_{x}\) is the probability of flipping the coin and having it land on heads (\(\rho_{heads}\)) or tails (\(\rho_{tails}\))
• \(H_A: \rho_{heads} \neq \rho_{tails}\)

When we conduct hypothesis testing, the statistical models calculate a p-value, which shows how likely we are to observe the data if the null hypothesis is true. If the p-value (a probability between 0 and 1) is small, we have strong evidence to reject the null hypothesis, as it is unlikely to see the data we observe if the null hypothesis is true. However, if the p-value is large, we say we do not have evidence to reject the null hypothesis. The size of the p-value for this cut-off is determined by Type 1 error known as \(\alpha\). A common Type 1 error value for statistical testing is to use \(\alpha = 0.05\)¹². Explanations of statistical testing often refer to confidence level. The confidence level is the inverse of the Type 1 error. Thus, if \(\alpha = 0.05\), the confidence level would be 95%.

The functions in the {survey} package allow for the correct estimation of the uncertainty estimates (e.g., standard deviations and confidence intervals). This chapter covers the following statistical tests with survey data and the following functions from the {survey} package (Lumley 2010):

• Comparison of proportions (svyttest())
• Comparison of means (svyttest())
• Goodness-of-fit tests (svygofchisq())
• Tests of independence (svychisq())
• Tests of homogeneity (svychisq())

6.2 Dot notation

Up to this point, we have shown functions that use wrappers from the {srvyr} package. This means that the functions work with tidyverse syntax. However, the functions in this chapter do not have wrappers in the {srvyr} package and are instead used directly from the {survey} package. Therefore, the design object is not the first argument, and to use these functions with the magrittr pipe (%>%) and tidyverse syntax, we need to use dot (.) notation¹³.

Functions that work with the magrittr pipe (%>%) have the dataset as the first argument. When we run a function with the pipe, it automatically places anything to the left of the pipe into the first argument of the function to the right of the pipe. For example, if we wanted to take the towny data from the {gt} package and filter to municipalities with the Census Subdivision Type of “city,” we can write the code in at least four different ways:

1. filter(towny, csd_type == "city")
2. towny %>% filter(csd_type == "city")
3. towny %>% filter(., csd_type == "city")
4. towny %>% filter(.data = ., csd_type == "city")

Each of these lines of code produces the same output since the argument that takes the dataset is in the first spot in filter(). The first two are probably familiar to those who have worked with the tidyverse. The third option functions the same way as the second one but is explicit that towny goes into the first argument, and the fourth option indicates that towny is going into the named argument of .data. Here, we are telling R to take what is on the left side of the pipe (towny) and pipe it into the spot with the dot (.) — the first argument.

In functions that are not part of the tidyverse, the data argument may not be in the first spot. For example, in svyttest(), the data argument is in the second spot, which means we need to place the dot (.) in the second spot and not the first. For example:

svydata_des %>%
 svyttest(x ~ y, .)

By default, the pipe places the left-hand object in the first argument spot. Placing the dot (.) in the second argument spot indicates that the survey design object svydata_des should be used in the second argument and not the first.

Alternatively, named arguments could be used to place the dot first, as named arguments can appear at any location as in the following:

svydata_des %>%
 svyttest(design = ., x ~ y)

However, the following code does not work as the svyttest() function expects the formula as the first argument when arguments are not named:

svydata_des %>%
 svyttest(., x ~ y)

6.3 Comparison of proportions and means

We use t-tests to compare two proportions or means. T-tests allow us to determine if one proportion or mean is statistically different from another. They are commonly used to determine if a single estimate differs from a known value (e.g., 0 or 50%) or to compare two group means (e.g., North versus South). Comparing a single estimate to a known value is called a one-sample t-test, and we can set up the hypothesis test as follows:

• \(H_0: \mu = 0\) where \(\mu\) is the mean outcome and \(0\) is the value we are comparing it to
• \(H_A: \mu \neq 0\)

For comparing two estimates, this is called a two-sample t-test. We can set up the hypothesis test as follows:

• \(H_0: \mu_1 = \mu_2\) where \(\mu_i\) is the mean outcome for group \(i\)
• \(H_A: \mu_1 \neq \mu_2\)

Two-sample t-tests can also be paired or unpaired. If the data come from two different populations (e.g., North versus South), the t-test run is an unpaired or independent samples t-test. Paired t-tests occur when the data come from the same population. This is commonly seen with data from the same population in two different time periods (e.g., before and after an intervention).

The difference between t-tests with non-survey data and survey data is based on the underlying variance estimation difference. Chapter 10 provides a detailed overview of the math behind the mean and sampling error calculations for various sample designs. The functions in the {survey} package account for these nuances, provided the design object is correctly defined.

6.3.1 Syntax

When we do not have survey data, we can use the t.test() function from the {stats} package to run t-tests. This function does not allow for weights or the variance structure that need to be accounted for with survey data. Therefore, we need to use the svyttest() function from {survey} when using survey data. Many of the arguments are the same between the two functions, but there are a few key differences:

• We need to use the survey design object instead of the original data frame
• We can only use a formula and not separate x and y data
• The confidence level cannot be specified and is always set to 95%. However, we show examples of how the confidence level can be changed after running the svyttest() function by using the confint() function.

Here is the syntax for the svyttest() function:

svyttest(formula,
         design,
         ...)

The arguments are:

• formula: Formula, outcome~group for two-sample, outcome~0 or outcome~1 for one-sample. The group variable must be a factor or character with two levels, or be coded 0/1 or 1/2. We give more details on formula set-up below for different types of tests.
• design: survey design object
• ...: This passes options on for one-sided tests only, and thus, we can specify na.rm=TRUE

Notice that the first argument here is the formula and not the design. This means we must use the dot (.) if we pipe in the survey design object (as described in Section 6.2).

The formula argument can take several different forms depending on what we are measuring. Here are a few common scenarios:

1. One-sample t-test:
   1. Comparison to 0: var ~ 0, where var is the measure of interest, and we compare it to the value 0. For example, we could test if the population mean of household debt is different from 0 given the sample data collected.
   2. Comparison to a different value: var - value ~ 0, where var is the measure of interest and value is what we are comparing to. For example, we could test if the proportion of the population that has blue eyes is different from 25% by using var - 0.25 ~ 0. Note that specifying the formula as var ~ 0.25 is not equivalent and results in a syntax error.
2. Two-sample t-test:
   1. Unpaired:
      • 2 level grouping variable: var ~ groupVar, where var is the measure of interest and groupVar is a variable with two categories. For example, we could test if the average age of the population who voted for president in 2020 differed from the age of people who did not vote. In this case, age would be used for var, and a binary variable indicating voting activity would be the groupVar.
      • 3+ level grouping variable: var ~ groupVar == level, where var is the measure of interest, groupVar is the categorical variable, and level is the category level to isolate. For example, we could test if the test scores in one classroom differed from all other classrooms where groupVar would be the variable holding the values for classroom IDs and level is the classroom ID we want to compare to the others.
   2. Paired: var_1 - var_2 ~ 0, where var_1 is the first variable of interest and var_2 is the second variable of interest. For example, we could test if test scores on a subject differed between the start and the end of a course, so var_1 would be the test score at the beginning of the course, and var_2 would be the score at the end of the course.

The na.rm argument defaults to FALSE, which means if any data values are missing, the t-test does not compute. Throughout this chapter, we always set na.rm = TRUE, but before analyzing the survey data, review the notes provided in Chapter 11 to better understand how to handle missing data.

Let’s walk through a few examples using the RECS data.

6.3.2 Examples

Example 1: One-sample t-test for mean

RECS asks respondents to indicate what temperature they set their house to during the summer at night¹⁴. In our data, we have called this variable SummerTempNight. If we want to see if the average U.S. household sets its temperature at a value different from 68\(^\circ\)F¹⁵, we could set up the hypothesis as follows:

• \(H_0: \mu = 68\) where \(\mu\) is the average temperature U.S. households set their thermostat to in the summer at night
• \(H_A: \mu \neq 68\)

To conduct this in R, we use svyttest() and subtract the temperature on the left-hand side of the formula:

ttest_ex1 <- recs_des %>%
  svyttest(
    formula = SummerTempNight - 68 ~ 0,
    design = .,
    na.rm = TRUE
  )

ttest_ex1

## 
##  Design-based one-sample t-test
## 
## data:  SummerTempNight - 68 ~ 0
## t = 85, df = 58, p-value <2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  3.288 3.447
## sample estimates:
##  mean 
## 3.367

To pull out specific output, we can use R’s built-in $ operator. For instance, to obtain the estimate \(\mu - 68\), we run ttest_ex1$estimate.

If we want the average, we take our t-test estimate and add it to 68:

ttest_ex1$estimate + 68

##  mean 
## 71.37

Or, we can use the survey_mean() function described in Chapter 5:

recs_des %>%
  summarize(mu = survey_mean(SummerTempNight, na.rm = TRUE))

## # A tibble: 1 × 2
##      mu  mu_se
##   <dbl>  <dbl>
## 1  71.4 0.0397

The result is the same in both methods, so we see that the average temperature U.S. households set their thermostat to in the summer at night is 71.4\(^\circ\)F. Looking at the output from svyttest(), the t-statistic is 84.8, and the p-value is <0.0001, indicating that the average is statistically different from 68\(^\circ\)F at an \(\alpha\) level of \(0.05\).

If we want an 80% confidence interval for the test statistic, we can use the function confint() to change the confidence level. Below, we print the default confidence interval (95%), the confidence interval explicitly specifying the level as 95%, and the 80% confidence interval. When the confidence level is 95% either by default or explicitly, R returns a vector with both row and column names. However, when we specify any other confidence level, an unnamed vector is returned, with the first element being the lower bound and the second element being the upper bound of the confidence interval.

confint(ttest_ex1)

##                                  2.5 % 97.5 %
## as.numeric(SummerTempNight - 68) 3.288  3.447
## attr(,"conf.level")
## [1] 0.95

confint(ttest_ex1, level = 0.95)

##                                  2.5 % 97.5 %
## as.numeric(SummerTempNight - 68) 3.288  3.447
## attr(,"conf.level")
## [1] 0.95

confint(ttest_ex1, level = 0.8)

## [1] 3.316 3.419
## attr(,"conf.level")
## [1] 0.8

In this case, neither confidence interval contains 0, and we draw the same conclusion from either that the average temperature households set their thermostat in the summer at night is significantly higher than 68\(^\circ\)F.

Example 2: One-sample t-test for proportion

RECS asked respondents if they use air conditioning (A/C) in their home¹⁶. In our data, we call this variable ACUsed. Let’s look at the proportion of U.S. households that use A/C in their homes using the survey_prop() function we learned in Chapter 5.

acprop <- recs_des %>%
  group_by(ACUsed) %>%
  summarize(p = survey_prop())

acprop

## # A tibble: 2 × 3
##   ACUsed     p    p_se
##   <lgl>  <dbl>   <dbl>
## 1 FALSE  0.113 0.00306
## 2 TRUE   0.887 0.00306

Based on this, 88.7% of U.S. households use A/C in their homes. If we wanted to know if this differs from 90%, we could set up our hypothesis as follows:

• \(H_0: p = 0.90\) where \(p\) is the proportion of U.S. households that use A/C in their homes
• \(H_A: p \neq 0.90\)

To conduct this in R, we use the svyttest() function as follows:

ttest_ex2 <- recs_des %>%
  svyttest(
    formula = (ACUsed == TRUE) - 0.90 ~ 0,
    design = .,
    na.rm = TRUE
  )

ttest_ex2

## 
##  Design-based one-sample t-test
## 
## data:  (ACUsed == TRUE) - 0.9 ~ 0
## t = -4.4, df = 58, p-value = 5e-05
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  -0.019603 -0.007348
## sample estimates:
##     mean 
## -0.01348

The output from the svyttest() function can be a bit hard to read. Using the tidy() function from the {broom} package, we can clean up the output into a tibble to more easily understand what the test tells us (Robinson, Hayes, and Couch 2023).

tidy(ttest_ex2)

## # A tibble: 1 × 8
##   estimate statistic   p.value parameter conf.low conf.high method      
##      <dbl>     <dbl>     <dbl>     <dbl>    <dbl>     <dbl> <chr>       
## 1  -0.0135     -4.40 0.0000466        58  -0.0196  -0.00735 Design-base…
## # ℹ 1 more variable: alternative <chr>

The ‘tidied’ output can also be piped into the {gt} package to create a table ready for publication (see Table 6.1). We go over the {gt} package in Chapter 8. The function pretty_p_value() comes from the {prettyunits} package and converts numeric p-values to characters and, by default, prints four decimal places and displays any p-value less than 0.0001 as "<0.0001", though another minimum display p-value can be specified (Csardi 2023).

tidy(ttest_ex2) %>%
  mutate(p.value = pretty_p_value(p.value)) %>%
  gt() %>%
  fmt_number()

TABLE 6.1: One-sample t-test output for estimates of U.S. households use A/C in their homes differing from 90%, RECS 2020

estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
−0.01	−4.40	<0.0001	58.00	−0.02	−0.01	Design-based one-sample t-test	two.sided

The estimate differs from Example 1 in that it does not display \(p - 0.90\) but rather \(p\), or the difference between the U.S. households that use A/C and our comparison proportion. We can see that there is a difference of —1.35 percentage points. Additionally, the t-statistic value in the statistic column is —4.4, and the p-value is <0.0001. These results indicate that fewer than 90% of U.S. households use A/C in their homes.

Example 3: Unpaired two-sample t-test

In addition to ACUsed, another variable in the RECS data is a household’s total electric cost in dollars (DOLLAREL).To see if U.S. households with A/C had higher electrical bills than those without, we can set up the hypothesis as follows:

• \(H_0: \mu_{AC} = \mu_{noAC}\) where \(\mu_{AC}\) is the electrical bill cost for U.S. households that used A/C, and \(\mu_{noAC}\) is the electrical bill cost for U.S. households that did not use A/C
• \(H_A: \mu_{AC} \neq \mu_{noAC}\)

Let’s take a quick look at the data to see how they are formatted:

recs_des %>%
  group_by(ACUsed) %>%
  summarize(mean = survey_mean(DOLLAREL, na.rm = TRUE))

## # A tibble: 2 × 3
##   ACUsed  mean mean_se
##   <lgl>  <dbl>   <dbl>
## 1 FALSE  1056.   16.0 
## 2 TRUE   1422.    5.69

To conduct this in R, we use svyttest():

ttest_ex3 <- recs_des %>%
  svyttest(
    formula = DOLLAREL ~ ACUsed,
    design = .,
    na.rm = TRUE
  )

tidy(ttest_ex3) %>%
  mutate(p.value = pretty_p_value(p.value)) %>%
  gt() %>%
  fmt_number()

TABLE 6.2: Unpaired two-sample t-test output for estimates of U.S. households electrical bills by A/C use, RECS 2020

estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
365.72	21.29	<0.0001	58.00	331.33	400.11	Design-based t-test	two.sided

The results in Table 6.2 indicate that the difference in electrical bills for those who used A/C and those who did not is, on average, $365.72. The difference appears to be statistically significant as the t-statistic is 21.3 and the p-value is <0.0001. Households that used A/C spent, on average, $365.72 more in 2020 on electricity than households without A/C.

Example 4: Paired two-sample t-test

Let’s say we want to test whether the temperature at which U.S. households set their thermostat at night differs depending on the season (comparing summer and winter¹⁷ temperatures). We could set up the hypothesis as follows:

• \(H_0: \mu_{summer} = \mu_{winter}\) where \(\mu_{summer}\) is the temperature that U.S. households set their thermostat to during summer nights, and \(\mu_{winter}\) is the temperature that U.S. households set their thermostat to during winter nights
• \(H_A: \mu_{summer} \neq \mu_{winter}\)

To conduct this in R, we use svyttest() by calculating the temperature difference on the left-hand side as follows:

ttest_ex4 <- recs_des %>%
  svyttest(
    design = .,
    formula = SummerTempNight - WinterTempNight ~ 0,
    na.rm = TRUE
  )

tidy(ttest_ex4) %>%
  mutate(p.value = pretty_p_value(p.value)) %>%
  gt() %>%
  fmt_number()

TABLE 6.3: Paired two-sample t-test output for estimates of U.S. households thermostat temperature by season, RECS 2020

estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
2.85	50.83	<0.0001	58.00	2.74	2.96	Design-based one-sample t-test	two.sided

The results displayed in Table 6.3 indicate that U.S. households set their thermostat on average 2.9\(^\circ\)F warmer in summer nights than winter nights, which is statistically significant (t = 50.8, p-value is <0.0001).

6.4 Chi-squared tests

Chi-squared tests (\(\chi^2\)) allow us to examine multiple proportions using a goodness-of-fit test, a test of independence, or a test of homogeneity. These three tests have the same \(\chi^2\) distributions but with slightly different underlying assumptions.

First, goodness-of-fit tests are used when comparing observed data to expected data. For example, this could be used to determine if respondent demographics (the observed data in the sample) match known population information (the expected data). In this case, we can set up the hypothesis test as follows:

• \(H_0: p_1 = \pi_1, ~ p_2 = \pi_2, ~ ..., ~ p_k = \pi_k\) where \(p_i\) is the observed proportion for category \(i\), \(\pi_i\) is the expected proportion for category \(i\), and \(k\) is the number of categories
• \(H_A:\) at least one level of \(p_i\) does not match \(\pi_i\)

Second, tests of independence are used when comparing two types of observed data to see if there is a relationship. For example, this could be used to determine if the proportion of respondents who voted for each political party in the presidential election matches the proportion of respondents who voted for each political party in a local election. In this case, we can set up the hypothesis test as follows:

• \(H_0:\) The two variables/factors are independent
• \(H_A:\) The two variables/factors are not independent

Third, tests of homogeneity are used to compare two distributions to see if they match. For example, this could be used to determine if the highest education achieved is the same for both men and women. In this case, we can set up the hypothesis test as follows:

• \(H_0: p_{1a} = p_{1b}, ~ p_{2a} = p_{2b}, ~ ..., ~ p_{ka} = p_{kb}\) where \(p_{ia}\) is the observed proportion of category \(i\) for subgroup \(a\), \(p_{ib}\) is the observed proportion of category \(i\) for subgroup \(a\), and \(k\) is the number of categories
• \(H_A:\) at least one category of \(p_{ia}\) does not match \(p_{ib}\)

As with t-tests, the difference between using \(\chi^2\) tests with non-survey data and survey data is based on the underlying variance estimation. The functions in the {survey} package account for these nuances, provided the design object is correctly defined. For basic variance estimation formulas for different survey design types, refer to Chapter 10.

6.4.1 Syntax

When we do not have survey data, we may be able to use the chisq.test() function from the {stats} package in base R to run chi-squared tests (R Core Team 2024). However, this function does not allow for weights or the variance structure to be accounted for with survey data. Therefore, when using survey data, we need to use one of two functions:

• svygofchisq(): For goodness-of-fit tests
• svychisq(): For tests of independence and homogeneity

The non-survey data function of chisq.test() requires either a single set of counts and given proportions (for goodness-of-fit tests) or two sets of counts for tests of independence and homogeneity. The functions we use with survey data require respondent-level data and formulas instead of counts. This ensures that the variances are correctly calculated.

First, the function for the goodness-of-fit tests is svygofchisq():

svygofchisq(formula,
            p,
            design,
            na.rm = TRUE,
            ...)

The arguments are:

• formula: Formula specifying a single factor variable
• p: Vector of probabilities for the categories of the factor in the correct order. If the probabilities do not sum to 1, they are rescaled to sum to 1.
• design: Survey design object
• …: Other arguments to pass on, such as na.rm

Based on the order of the arguments, we again must use the dot (.) notation if we pipe in the survey design object or explicitly name the arguments as described in Section 6.2. For the goodness-of-fit tests, the formula is a single variable formula = ~var as we compare the observed data from this variable to the expected data. The expected probabilities are then entered in the p argument and need to be a vector of the same length as the number of categories in the variable. For example, if we want to know if the proportion of males and females matches a distribution of 30/70, then the sex variable (with two categories) would be used formula = ~SEX, and the proportions would be included as p = c(.3, .7). It is important to note that the variable entered into the formula should be formatted as either a factor or a character. The examples below provide more detail and tips on how to make sure the levels match up correctly.

For tests of homogeneity and independence, the svychisq() function should be used. The syntax is as follows:

svychisq(
  formula,
  design,
  statistic = c("F", "Chisq", "Wald", "adjWald",
                "lincom", "saddlepoint"),
  na.rm = TRUE
)

The arguments are:

• formula: Model formula specifying the table (shown in examples)
• design: Survey design object
• statistic: Type of test statistic to use in test (details below)
• na.rm: Remove missing values

There are six statistics that are accepted in this formula. For tests of homogeneity (when comparing cross-tabulations), the F or Chisq statistics should be used¹⁸. The F statistic is the default and uses the Rao-Scott second-order correction. This correction is designed to assist with complicated sampling designs (i.e., those other than a simple random sample) (Scott 2007). The Chisq statistic is an adjusted version of the Pearson \(\chi^2\) statistic. The version of this statistic in the svychisq() function compares the design effect estimate from the provided survey data to what the \(\chi^2\) distribution would have been if the data came from a simple random sampling.

For tests of independence, the Wald and adjWald are recommended as they provide a better adjustment for variable comparisons (Lumley 2010). If the data have a small number of primary sampling units (PSUs) compared to the degrees of freedom, then the adjWald statistic should be used to account for this. The lincom and saddlepoint statistics are available for more complicated data structures.

The formula argument is always one-sided, unlike the svyttest() function. The two variables of interest should be included with a plus sign: formula = ~ var_1 + var_2. As with the svygofchisq() function, the variables entered into the formula should be formatted as either a factor or a character.

Additionally, as with the t-test function, both svygofchisq() and svychisq() have the na.rm argument. If any data values are missing, the \(\chi^2\) tests assume that NA is a category and include it in the calculation. Throughout this chapter, we always set na.rm = TRUE, but before analyzing the survey data, review the notes provided in Chapter 11 to better understand how to handle missing data.

6.4.2 Examples

Let’s walk through a few examples using the ANES data.

Example 1: Goodness-of-fit test

ANES asked respondents about their highest education level¹⁹. Based on the data from the 2020 American Community Survey (ACS) 5-year estimates²⁰, the education distribution of those aged 18+ in the United States (among the 50 states and the District of Columbia) is as follows:

• 11% had less than a high school degree
• 27% had a high school degree
• 29% had some college or an associate’s degree
• 33% had a bachelor’s degree or higher

If we want to see if the weighted distribution from the ANES 2020 data matches this distribution, we could set up the hypothesis as follows:

• \(H_0: p_1 = 0.11, ~ p_2 = 0.27, ~ p_3 = 0.29, ~ p_4 = 0.33\)
• \(H_A:\) at least one of the education levels does not match between the ANES and the ACS

To conduct this in R, let’s first look at the education variable (Education) we have on the ANES data. Using the survey_mean() function discussed in Chapter 5, we can see the education levels and estimated proportions.

anes_des %>%
  drop_na(Education) %>%
  group_by(Education) %>%
  summarize(p = survey_mean())

## # A tibble: 5 × 3
##   Education         p    p_se
##   <fct>         <dbl>   <dbl>
## 1 Less than HS 0.0805 0.00568
## 2 High school  0.277  0.0102 
## 3 Post HS      0.290  0.00713
## 4 Bachelor's   0.226  0.00633
## 5 Graduate     0.126  0.00499

Based on this output, we can see that we have different levels from the ACS data. Specifically, the education data from ANES include two levels for bachelor’s degree or higher (bachelor’s and graduate), so these two categories need to be collapsed into a single category to match the ACS data. For this, among other methods, we can use the {forcats} package from the tidyverse (Wickham 2023). The package’s fct_collapse() function helps us create a new variable by collapsing categories into a single one. Then, we use the svygofchisq() function to compare the ANES data to the ACS data, where we specify the updated design object, the formula using the collapsed education variable, the ACS estimates for education levels as p, and removing NA values.

anes_des_educ <- anes_des %>%
  mutate(
    Education2 =
      fct_collapse(Education,
        "Bachelor or Higher" = c(
          "Bachelor's",
          "Graduate"
        )
      )
  )

anes_des_educ %>%
  drop_na(Education2) %>%
  group_by(Education2) %>%
  summarize(p = survey_mean())

## # A tibble: 4 × 3
##   Education2              p    p_se
##   <fct>               <dbl>   <dbl>
## 1 Less than HS       0.0805 0.00568
## 2 High school        0.277  0.0102 
## 3 Post HS            0.290  0.00713
## 4 Bachelor or Higher 0.352  0.00732

chi_ex1 <- anes_des_educ %>%
  svygofchisq(
    formula = ~Education2,
    p = c(0.11, 0.27, 0.29, 0.33),
    design = .,
    na.rm = TRUE
  )

chi_ex1

## 
##  Design-based chi-squared test for given probabilities
## 
## data:  ~Education2
## X-squared = 2172220, scale = 1.1e+05, df = 2.3e+00, p-value =
## 9e-05

The output from the svygofchisq() indicates that at least one proportion from ANES does not match the ACS data (\(\chi^2 =\) 2,172,220; p-value is <0.0001). To get a better idea of the differences, we can use the expected output along with survey_mean() to create a comparison table:

ex1_table <- anes_des_educ %>%
  drop_na(Education2) %>%
  group_by(Education2) %>%
  summarize(Observed = survey_mean(vartype = "ci")) %>%
  rename(Education = Education2) %>%
  mutate(Expected = c(0.11, 0.27, 0.29, 0.33)) %>%
  select(Education, Expected, everything())

ex1_table

## # A tibble: 4 × 5
##   Education          Expected Observed Observed_low Observed_upp
##   <fct>                 <dbl>    <dbl>        <dbl>        <dbl>
## 1 Less than HS           0.11   0.0805       0.0691       0.0919
## 2 High school            0.27   0.277        0.257        0.298 
## 3 Post HS                0.29   0.290        0.276        0.305 
## 4 Bachelor or Higher     0.33   0.352        0.337        0.367

This output includes our expected proportions from the ACS that we provided the svygofchisq() function along with the output of the observed proportions and their confidence intervals. This table shows that the “high school” and “post HS” categories have nearly identical proportions, but that the other two categories are slightly different. Looking at the confidence intervals, we can see that the ANES data skew to include fewer people in the “less than HS” category and more people in the “bachelor or higher” category. This may be easier to see if we plot this. The code below uses the tabular output to create Figure 6.1.

ex1_table %>%
  pivot_longer(
    cols = c("Expected", "Observed"),
    names_to = "Names",
    values_to = "Proportion"
  ) %>%
  mutate(
    Observed_low = if_else(Names == "Observed", Observed_low, NA_real_),
    Observed_upp = if_else(Names == "Observed", Observed_upp, NA_real_),
    Names = if_else(Names == "Observed",
      "ANES (observed)", "ACS (expected)"
    )
  ) %>%
  ggplot(aes(x = Education, y = Proportion, color = Names)) +
  geom_point(alpha = 0.75, size = 2) +
  geom_errorbar(aes(ymin = Observed_low, ymax = Observed_upp),
    width = 0.25
  ) +
  theme_bw() +
  scale_color_manual(name = "Type", values = book_colors[c(4, 1)]) +
  theme(legend.position = "bottom", legend.title = element_blank())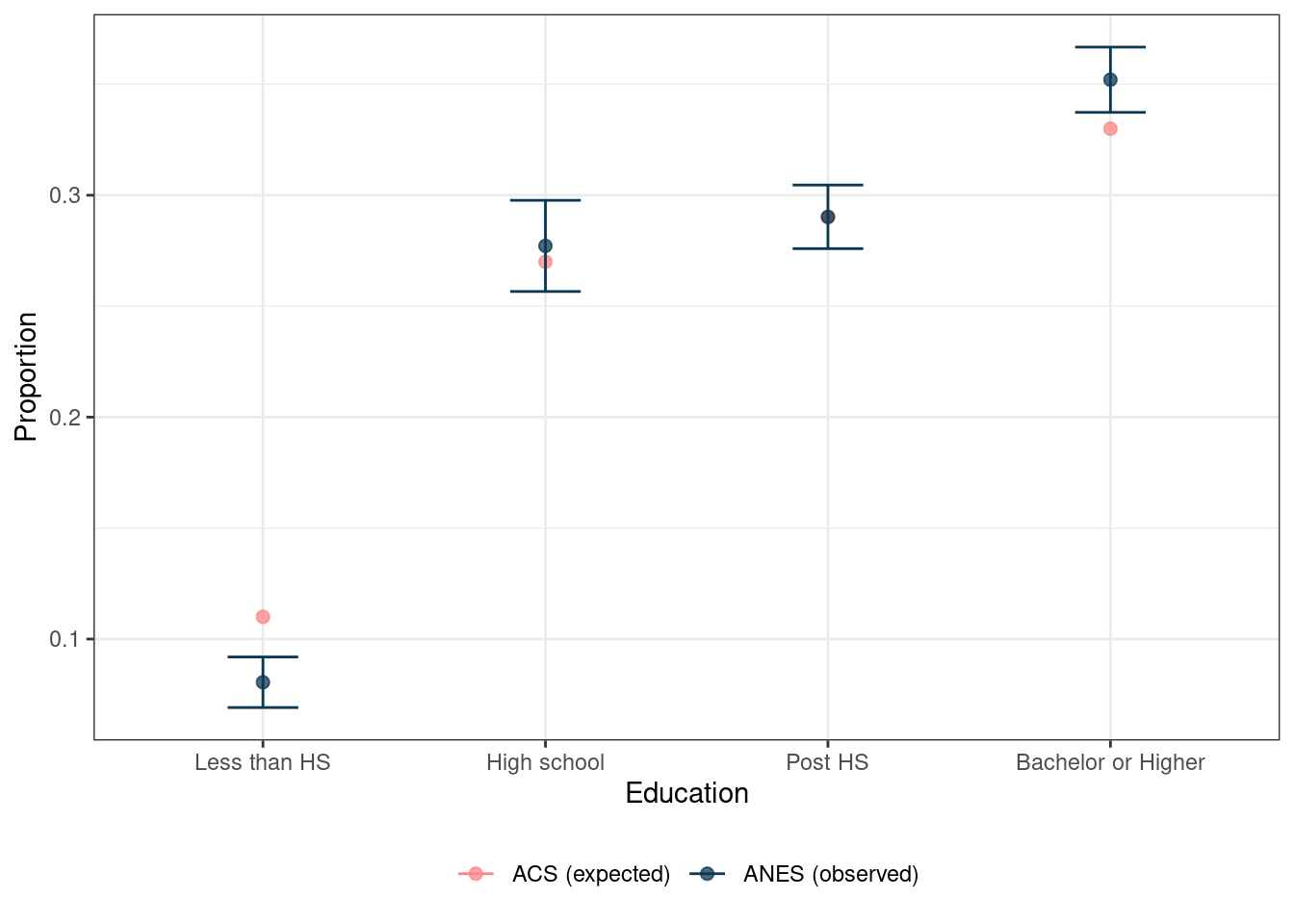

FIGURE 6.1: Expected and observed proportions of education with confidence intervals

Example 2: Test of independence

ANES asked respondents two questions about trust:

• Question text: “How often can you trust the federal government to do what is right?” (American National Election Studies 2021)
• Question text: “How often can you trust other people?” (American National Election Studies 2021)

If we want to see if the distributions of these two questions are similar or not, we can conduct a test of independence. Here is how the hypothesis could be set up:

• \(H_0:\) People’s trust in the federal government and their trust in other people are independent (i.e., not related)
• \(H_A:\) People’s trust in the federal government and their trust in other people are not independent (i.e., they are related)

To conduct this in R, we use the svychisq() function to compare the two variables:

chi_ex2 <- anes_des %>%
  svychisq(
    formula = ~ TrustGovernment + TrustPeople,
    design = .,
    statistic = "Wald",
    na.rm = TRUE
  )

chi_ex2

## 
##  Design-based Wald test of association
## 
## data:  NextMethod()
## F = 21, ndf = 16, ddf = 51, p-value <2e-16

The output from svychisq() indicates that the distribution of people’s trust in the federal government and their trust in other people are not independent, meaning that they are related. Let’s output the distributions in a table to see the relationship. The observed output from the test provides a cross-tabulation of the counts for each category:

chi_ex2$observed

##                      TrustPeople
## TrustGovernment         Always Most of the time About half the time
##   Always                16.470           25.009              31.848
##   Most of the time      11.020          539.377             196.258
##   About half the time   11.772          934.858             861.971
##   Some of the time      17.007         1353.779             839.863
##   Never                  3.174          236.785             174.272
##                      TrustPeople
## TrustGovernment       Some of the time    Never
##   Always                        36.854    5.523
##   Most of the time             206.556   27.184
##   About half the time          428.871   65.024
##   Some of the time             932.628   89.596
##   Never                        217.994  189.307

However, we often want to know about the proportions, not just the respondent counts from the survey. There are a couple of different ways that we can do this. The first is using the counts from chi_ex2$observed to calculate the proportion. We can then pivot the table to create a cross-tabulation similar to the counts table above. Adding group_by() to the code means that we obtain the proportions within each variable level. In this case, we are looking at the distribution of TrustGovernment for each level of TrustPeople. The resulting table is shown in Table 6.4.

chi_ex2_table <- chi_ex2$observed %>%
  as_tibble() %>%
  group_by(TrustPeople) %>%
  mutate(prop = round(n / sum(n), 3)) %>%
  select(-n) %>%
  pivot_wider(names_from = TrustPeople, values_from = prop) %>%
  gt(rowname_col = "TrustGovernment") %>%
  tab_stubhead(label = "Trust in Government") %>%
  tab_spanner(
    label = "Trust in People",
    columns = everything()
  ) %>%
  cols_label(
    `Most of the time` = md("Most of<br />the time"),
    `About half the time` = md("About half<br />the time"),
    `Some of the time` = md("Some of<br />the time")
  )

chi_ex2_table

TABLE 6.4: Proportion of adults in the U.S. by levels of trust in people and government, ANES 2020

Trust in Government	Trust in People
	Always	Most of the time	About half the time	Some of the time	Never
Always	0.277	0.008	0.015	0.020	0.015
Most of the time	0.185	0.175	0.093	0.113	0.072
About half the time	0.198	0.303	0.410	0.235	0.173
Some of the time	0.286	0.438	0.399	0.512	0.238
Never	0.053	0.077	0.083	0.120	0.503

In Table 6.4, each column sums to 1. For example, we can say that it is estimated that of people who always trust in people, 27.7% also always trust in the government based on the top-left cell, but 5.3% never trust in the government.

The second option is to use the group_by() and survey_mean() functions to calculate the proportions from the ANES design object. Remember that with more than one variable listed in the group_by() statement, the proportions are within the first variable listed. As mentioned above, we are looking at the distribution of TrustGovernment for each level of TrustPeople.

chi_ex2_obs <- anes_des %>%
  drop_na(TrustPeople, TrustGovernment) %>%
  group_by(TrustPeople, TrustGovernment) %>%
  summarize(
    Observed = round(survey_mean(vartype = "ci"), 3),
    .groups = "drop"
  )

chi_ex2_obs_table <- chi_ex2_obs %>%
  mutate(prop = paste0(
    Observed, " (", Observed_low, ", ",
    Observed_upp, ")"
  )) %>%
  select(TrustGovernment, TrustPeople, prop) %>%
  pivot_wider(names_from = TrustPeople, values_from = prop) %>%
  gt(rowname_col = "TrustGovernment") %>%
  tab_stubhead(label = "Trust in Government") %>%
  tab_spanner(
    label = "Trust in People",
    columns = everything()
  ) %>%
  tab_options(page.orientation = "landscape")

chi_ex2_obs_table

TABLE 6.5: Proportion of adults in the U.S. by levels of trust in people and government with confidence intervals, ANES 2020

Trust in Government	Trust in People
	Always	Most of the time	About half the time	Some of the time	Never
Always	0.277 (0.11, 0.444)	0.008 (0.004, 0.012)	0.015 (0.006, 0.024)	0.02 (0.008, 0.033)	0.015 (0, 0.029)
Most of the time	0.185 (-0.009, 0.38)	0.175 (0.157, 0.192)	0.093 (0.078, 0.109)	0.113 (0.085, 0.141)	0.072 (0.021, 0.123)
About half the time	0.198 (0.046, 0.35)	0.303 (0.281, 0.324)	0.41 (0.378, 0.441)	0.235 (0.2, 0.271)	0.173 (0.099, 0.246)
Some of the time	0.286 (0.069, 0.503)	0.438 (0.415, 0.462)	0.399 (0.365, 0.433)	0.512 (0.481, 0.543)	0.238 (0.178, 0.298)
Never	0.053 (-0.01, 0.117)	0.077 (0.064, 0.089)	0.083 (0.063, 0.103)	0.12 (0.097, 0.142)	0.503 (0.422, 0.583)

Both methods produce the same output as the svychisq() function. However, calculating the proportions directly from the design object allows us to obtain the variance information. In this case, the output in Table 6.5 displays the survey estimate followed by the confidence intervals. Based on the output, we can see that of those who never trust people, 50.3% also never trust the government, while the proportions of never trusting the government are much lower for each of the other levels of trusting people.

We may find it easier to look at these proportions graphically. We can use ggplot() and facets to provide an overview to create Figure 6.2 below:

chi_ex2_obs %>%
  mutate(
    TrustPeople =
      fct_reorder(
        str_c("Trust in People:\n", TrustPeople),
        order(TrustPeople)
      )
  ) %>%
  ggplot(
    aes(x = TrustGovernment, y = Observed, color = TrustGovernment)
  ) +
  facet_wrap(~TrustPeople, ncol = 5) +
  geom_point() +
  geom_errorbar(aes(ymin = Observed_low, ymax = Observed_upp)) +
  ylab("Proportion") +
  xlab("") +
  theme_bw() +
  scale_color_manual(
    name = "Trust in Government",
    values = book_colors
  ) +
  theme(
    axis.text.x = element_blank(),
    axis.ticks.x = element_blank(),
    legend.position = "bottom"
  ) +
  guides(col = guide_legend(nrow = 2))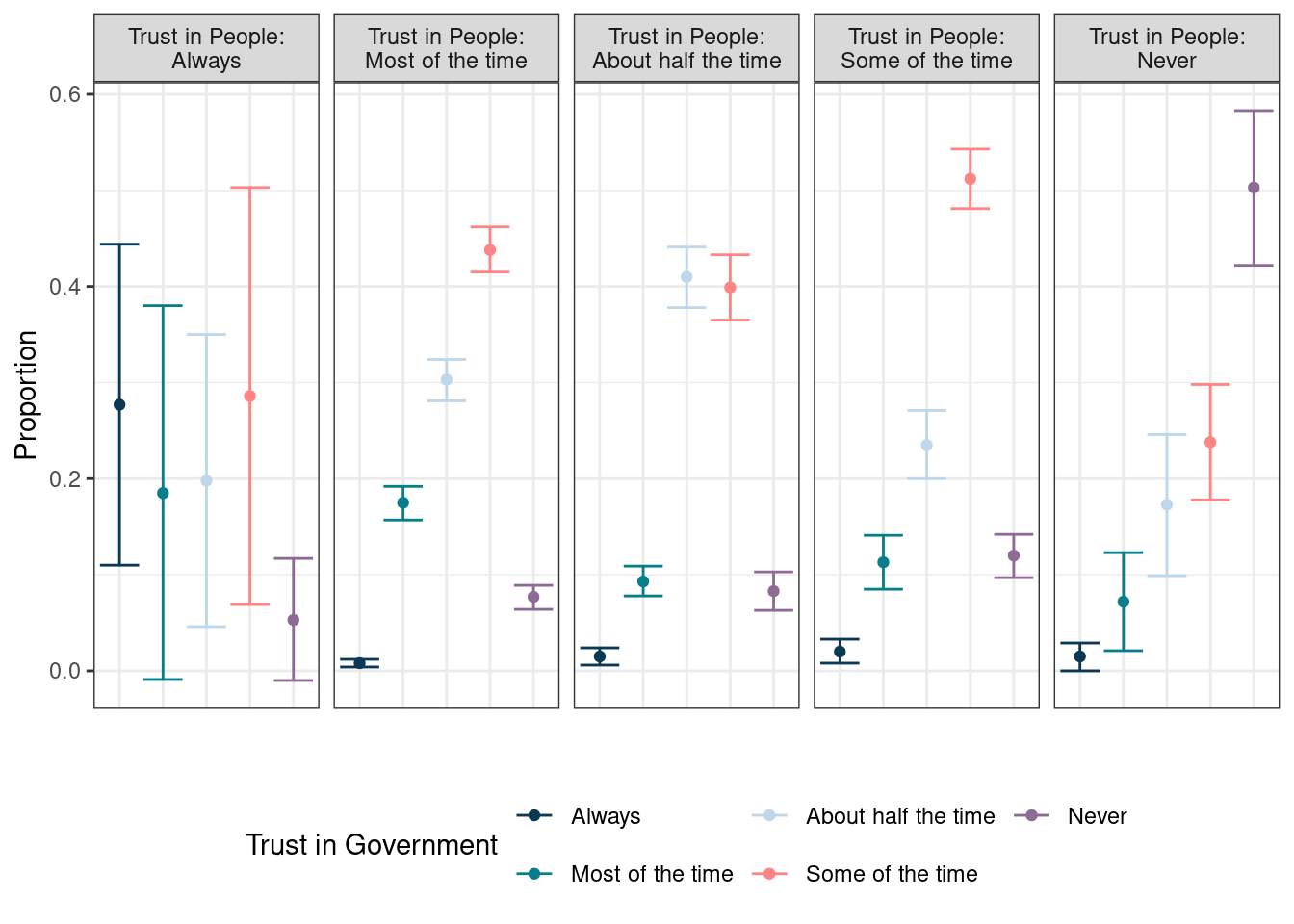

FIGURE 6.2: Proportion of adults in the U.S. by levels of trust in people and government with confidence intervals, ANES 2020

Example 3: Test of homogeneity

Researchers and politicians often look at specific demographics each election cycle to understand how each group is leaning or voting toward candidates. The ANES data are collected post-election, but we can still see if there are differences in how specific demographic groups voted.

If we want to see if there is a difference in how each age group voted for the 2020 candidates, this would be a test of homogeneity, and we can set up the hypothesis as follows:

\[\begin{align*} H_0: p_{1_{Biden}} &= p_{1_{Trump}} = p_{1_{Other}},\\ p_{2_{Biden}} &= p_{2_{Trump}} = p_{2_{Other}},\\ p_{3_{Biden}} &= p_{3_{Trump}} = p_{3_{Other}},\\ p_{4_{Biden}} &= p_{4_{Trump}} = p_{4_{Other}},\\ p_{5_{Biden}} &= p_{5_{Trump}} = p_{5_{Other}},\\ p_{6_{Biden}} &= p_{6_{Trump}} = p_{6_{Other}} \end{align*}\] where \(p_{i_{Biden}}\) is the observed proportion of each age group (\(i\)) that voted for Joseph Biden, \(p_{i_{Trump}}\) is the observed proportion of each age group (\(i\)) that voted for Donald Trump, and \(p_{i_{Other}}\) is the observed proportion of each age group (\(i\)) that voted for another candidate.

• \(H_A:\) at least one category of \(p_{i_{Biden}}\) does not match \(p_{i_{Trump}}\) or \(p_{i_{Other}}\)

To conduct this in R, we use the svychisq() function to compare the two variables:

chi_ex3 <- anes_des %>%
  drop_na(VotedPres2020_selection, AgeGroup) %>%
  svychisq(
    formula = ~ AgeGroup + VotedPres2020_selection,
    design = .,
    statistic = "Chisq",
    na.rm = TRUE
  )

chi_ex3

## 
##  Pearson's X^2: Rao & Scott adjustment
## 
## data:  NextMethod()
## X-squared = 171, df = 10, p-value <2e-16

The output from svychisq() indicates a difference in how each age group voted in the 2020 election. To get a better idea of the different distributions, let’s output proportions to see the relationship. As we learned in Example 2 above, we can use chi_ex3$observed, or if we want to get the variance information (which is crucial with survey data), we can use survey_mean(). Remember, when we have two variables in group_by(), we obtain the proportions within each level of the variable listed. In this case, we are looking at the distribution of AgeGroup for each level of VotedPres2020_selection.

chi_ex3_obs <- anes_des %>%
  filter(VotedPres2020 == "Yes") %>%
  drop_na(VotedPres2020_selection, AgeGroup) %>%
  group_by(VotedPres2020_selection, AgeGroup) %>%
  summarize(Observed = round(survey_mean(vartype = "ci"), 3))

chi_ex3_obs_table <- chi_ex3_obs %>%
  mutate(prop = paste0(
    Observed, " (", Observed_low, ", ",
    Observed_upp, ")"
  )) %>%
  select(AgeGroup, VotedPres2020_selection, prop) %>%
  pivot_wider(
    names_from = VotedPres2020_selection,
    values_from = prop
  ) %>%
  gt(rowname_col = "AgeGroup") %>%
  tab_stubhead(label = "Age Group")

chi_ex3_obs_table

TABLE 6.6: Distribution of age group by presidential candidate selection with confidence intervals

Age Group	Biden	Trump	Other
18-29	0.203 (0.177, 0.229)	0.113 (0.095, 0.132)	0.221 (0.144, 0.298)
30-39	0.168 (0.152, 0.184)	0.146 (0.125, 0.168)	0.302 (0.21, 0.394)
40-49	0.163 (0.146, 0.18)	0.157 (0.137, 0.177)	0.21 (0.13, 0.29)
50-59	0.152 (0.135, 0.17)	0.229 (0.202, 0.256)	0.104 (0.04, 0.168)
60-69	0.177 (0.159, 0.196)	0.193 (0.173, 0.213)	0.103 (0.025, 0.182)
70 or older	0.136 (0.123, 0.149)	0.161 (0.143, 0.179)	0.06 (0.01, 0.109)

In Table 6.6 we can see that the age group distribution that voted for Biden and other candidates was younger than those that voted for Trump. For example, of those who voted for Biden, 20.4% were in the 18–29 age group, compared to only 11.4% of those who voted for Trump were in that age group. Conversely, 23.4% of those who voted for Trump were in the 50–59 age group compared to only 15.4% of those who voted for Biden.

6.5 Exercises

The exercises use the design objects anes_des and recs_des as provided in the Prerequisites box at the beginning of the chapter. Here are some exercises for practicing conducting t-tests using svyttest():

1. Using the RECS data, do more than 50% of U.S. households use A/C (ACUsed)?

2. Using the RECS data, does the average temperature at which U.S. households set their thermostats differ between the day and night in the winter (WinterTempDay and WinterTempNight)?

3. Using the ANES data, does the average age (Age) of those who voted for Joseph Biden in 2020 (VotedPres2020_selection) differ from those who voted for another candidate?

4. If we wanted to determine if the political party affiliation differed for males and females, what test would we use?

1. Goodness-of-fit test (svygofchisq())
2. Test of independence (svychisq())
3. Test of homogeneity (svychisq())

5. In the RECS data, is there a relationship between the type of housing unit (HousingUnitType) and the year the house was built (YearMade)?

6. In the ANES data, is there a difference in the distribution of gender (Gender) across early voting status in 2020 (EarlyVote2020)?

References

American National Election Studies. 2021. “ANES 2020 Time Series Study: Pre-Election and Post-Election Survey Questionnaires.” https://electionstudies.org/wp-content/uploads/2021/07/anes_timeseries_2020_questionnaire_20210719.pdf.

Csardi, Gabor. 2023. prettyunits: Pretty, Human Readable Formatting of Quantities. https://github.com/r-lib/prettyunits.

Lumley, Thomas. 2010. Complex Surveys: A Guide to Analysis Using R. John Wiley & Sons.

R Core Team. 2024. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Robinson, David, Alex Hayes, and Simon Couch. 2023. broom: Convert Statistical Objects into Tidy Tibbles. https://broom.tidymodels.org/.

Scott, Alastair. 2007. “Rao-Scott Corrections and Their Impact.” In Section on Survey Research Methods, 3514–18. http://www.asasrms.org/Proceedings/y2007/Files/JSM2007-000874.pdf.

———. 2020. “Residential Energy Consumption Survey (RECS) Form EIA-457A 2020 Household Questionnaire.” https://www.eia.gov/survey/form/eia_457/archive/2020_RECS-457A.pdf.

———. 2023. forcats: Tools for Working with Categorical Variables (Factors). https://forcats.tidyverse.org/.

---

12. For more information on statistical testing, we recommend reviewing introduction to statistics textbooks.↩︎

13. This could change in the future if another package is built or {srvyr} is expanded to work with {tidymodels} packages, but no such plans are known at this time.↩︎

14. Question text: “During the summer, what is your home’s typical indoor temperature inside your home at night?” (U.S. Energy Information Administration 2020)↩︎

15. This is the temperature that Stephanie prefers at night during the summer, and she wanted to see if she was different from the population.↩︎

16. Question text: “Is any air conditioning equipment used in your home?” (U.S. Energy Information Administration 2020)↩︎

17. Question text: “During the winter, what is your home’s typical indoor temperature inside your home at night?” (U.S. Energy Information Administration 2020)↩︎

18. These two statistics can also be used for goodness-of-fit tests if the svygofchisq() function is not used.↩︎

19. Question text: “What is the highest level of school you have completed or the highest degree you have received?” (American National Election Studies 2021)↩︎

20. Data was pulled from data.census.gov using the S1501 Education Attainment 2020: ACS 5-Year Estimates Subject Tables.↩︎