Chapter 12 Successful survey analysis recommendations
For this chapter, load the following packages:
To illustrate the importance of data visualization, we discuss Anscombe’s Quartet. The dataset can be replicated by running the code below:
anscombe_tidy <- anscombe %>%
mutate(obs = row_number()) %>%
pivot_longer(-obs, names_to = "key", values_to = "value") %>%
separate(key, c("variable", "set"), 1, convert = TRUE) %>%
mutate(set = c("I", "II", "III", "IV")[set]) %>%
pivot_wider(names_from = variable, values_from = value)We create an example survey dataset to explain potential pitfalls and how to overcome them in survey analysis. To recreate the dataset, run the code below:
example_srvy <- tribble(
~id, ~region, ~q_d1, ~q_d2_1, ~gender, ~weight,
1L, 1L, 1L, "Somewhat interested", "female", 1740,
2L, 1L, 1L, "Not at all interested", "female", 1428,
3L, 2L, NA, "Somewhat interested", "female", 496,
4L, 2L, 1L, "Not at all interested", "female", 550,
5L, 3L, 1L, "Somewhat interested", "female", 1762,
6L, 4L, NA, "Very interested", "female", 1004,
7L, 4L, NA, "Somewhat interested", "female", 522,
8L, 3L, 2L, "Not at all interested", "female", 1099,
9L, 4L, 2L, "Somewhat interested", "female", 1295,
10L, 2L, 2L, "Somewhat interested", "male", 983
)
example_des <-
example_srvy %>%
as_survey_design(weights = weight)12.1 Introduction
The previous chapters in this book aimed to provide the technical skills and knowledge required for running survey analyses. This chapter builds upon the previously mentioned best practices to present a curated set of recommendations for running a successful survey analysis. We hope this list provides practical insights that assist in producing meaningful and reliable results.
12.2 Follow the survey analysis process
As we first introduced in Chapter 4, there are four main steps to successfully analyze survey data:
Create a
tbl_svyobject (a survey object) using:as_survey_design()oras_survey_rep()Subset data (if needed) using
filter()(to create subpopulations)Specify domains of analysis using
group_by()Within
summarize(), specify variables to calculate, including means, totals, proportions, quantiles, and more
The order of these steps matters in survey analysis. For example, if we need to subset the data, we must use filter() on our data after creating the survey design. If we do this before the survey design is created, we may not be correctly accounting for the study design, resulting in inaccurate findings.
Additionally, correctly identifying the survey design is one of the most important steps in survey analysis. Knowing the type of sample design (e.g., clustered, stratified) helps ensure the underlying error structure is correctly calculated and weights are correctly used. Learning about complex design factors such as clustering, stratification, and weighting is foundational to complex survey analysis, and we recommend that all analysts review Chapter 10 before creating their first design object. Reviewing the documentation (see Chapter 3) helps us understand what variables to use from the data.
Making sure to use the survey analysis functions from the {srvyr} and {survey} packages is also important in survey analysis. For example, using mean() and survey_mean() on the same data results in different findings and outputs. Each of the survey functions from {srvyr} and {survey} impacts standard errors and variance, and we cannot treat complex surveys as unweighted simple random samples if we want to produce unbiased estimates (Freedman Ellis and Schneider 2024; Lumley 2010).
12.3 Begin with descriptive analysis
When receiving a fresh batch of data, it is tempting to jump right into running models to find significant results. However, a successful data analyst begins by exploring the dataset. Chapter 11 talks about the importance of reviewing data when examining missing data patterns. In this chapter, we illustrate the value of reviewing all types of data. This involves running descriptive analysis on the dataset as a whole, as well as individual variables and combinations of variables. As described in Chapter 5, descriptive analyses should always precede statistical analysis to prevent avoidable (and potentially embarrassing) mistakes.
12.3.1 Table review
Even before applying weights, consider running cross-tabulations on the raw data. Cross-tabs can help us see if any patterns stand out that may be alarming or something worth further investigating.
For example, let’s explore the example survey dataset introduced in the Prerequisites box, example_srvy. We run the code below on the unweighted data to inspect the gender variable:
## # A tibble: 2 × 2
## gender n
## <chr> <int>
## 1 female 9
## 2 male 1The data show that females comprise 9 out of 10, or 90%, of the sample. Generally, we assume something close to a 50/50 split between male and female respondents in a population. The sizable female proportion could indicate either a unique sample or a potential error in the data. If we review the survey documentation and see this was a deliberate part of the design, we can continue our analysis using the appropriate methods. If this was not an intentional choice by the researchers, the results alert us that something may be incorrect in the data or our code, and we can verify if there’s an issue by comparing the results with the weighted means.
12.3.2 Graphical review
Tables provide a quick check of our assumptions, but there is no substitute for graphs and plots to visualize the distribution of data. We might miss outliers or nuances if we scan only summary statistics.
For example, Anscombe’s Quartet demonstrates the importance of visualization in analysis. Let’s say we have a dataset with x- and y-variables in an object called anscombe_tidy. Let’s take a look at how the dataset is structured:
## # A tibble: 6 × 4
## obs set x y
## <int> <chr> <dbl> <dbl>
## 1 1 I 10 8.04
## 2 1 II 10 9.14
## 3 1 III 10 7.46
## 4 1 IV 8 6.58
## 5 2 I 8 6.95
## 6 2 II 8 8.14We can begin by checking one set of variables. For Set I, the x-variables have an average of 9 with a standard deviation of 3.3; for y, we have an average of 7.5 with a standard deviation of 2.03. The two variables have a correlation of 0.81.
anscombe_tidy %>%
filter(set == "I") %>%
summarize(
x_mean = mean(x),
x_sd = sd(x),
y_mean = mean(y),
y_sd = sd(y),
correlation = cor(x, y)
)## # A tibble: 1 × 5
## x_mean x_sd y_mean y_sd correlation
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 9 3.32 7.50 2.03 0.816These are useful statistics. We can note that the data do not have high variability, and the two variables are strongly correlated. Now, let’s check all the sets (I-IV) in the Anscombe data. Notice anything interesting?
anscombe_tidy %>%
group_by(set) %>%
summarize(
x_mean = mean(x),
x_sd = sd(x, na.rm = TRUE),
y_mean = mean(y),
y_sd = sd(y, na.rm = TRUE),
correlation = cor(x, y)
)## # A tibble: 4 × 6
## set x_mean x_sd y_mean y_sd correlation
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 I 9 3.32 7.50 2.03 0.816
## 2 II 9 3.32 7.50 2.03 0.816
## 3 III 9 3.32 7.5 2.03 0.816
## 4 IV 9 3.32 7.50 2.03 0.817The summary results for these four sets are nearly identical! Based on this, we might assume that each distribution is similar. Let’s look at a graphical visualization to see if our assumption is correct (see Figure 12.1).
ggplot(anscombe_tidy, aes(x, y)) +
geom_point() +
facet_wrap(~set) +
geom_smooth(method = "lm", se = FALSE, alpha = 0.5) +
theme_minimal()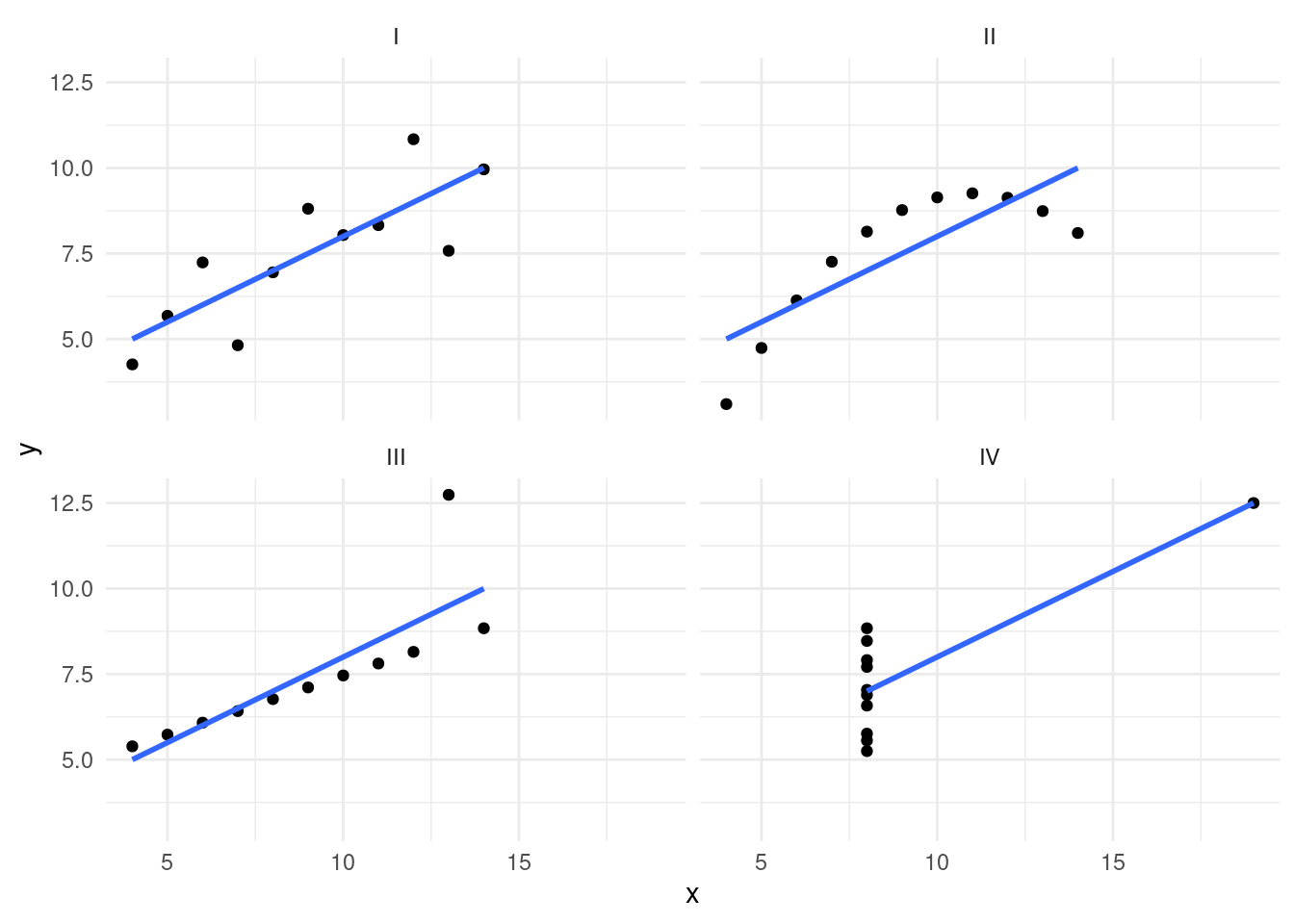
FIGURE 12.1: Plot of Anscombe’s Quartet data and the importance of reviewing data graphically
Although each of the four sets has the same summary statistics and regression line, when reviewing the plots (see Figure 12.1), it becomes apparent that the distributions of the data are not the same at all. Each set of points results in different shapes and distributions. Imagine sharing each set (I-IV) and the corresponding plot with a different colleague. The interpretations and descriptions of the data would be very different even though the statistics are similar. Plotting data can also ensure that we are using the correct analysis method on the data, so understanding the underlying distributions is an important first step.
12.4 Check variable types
When we pull the data from surveys into R, the data may be listed as character, factor, numeric, or logical/Boolean. The tidyverse functions that read in data (e.g., read_csv(), read_excel()) default to have all strings load as character variables. This is important when dealing with survey data, as many strings may be better suited for factors than character variables. For example, let’s revisit the example_srvy data. Taking a glimpse() of the data gives us insight into what it contains:
## Rows: 10
## Columns: 6
## $ id <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
## $ region <int> 1, 1, 2, 2, 3, 4, 4, 3, 4, 2
## $ q_d1 <int> 1, 1, NA, 1, 1, NA, NA, 2, 2, 2
## $ q_d2_1 <chr> "Somewhat interested", "Not at all interested", "Somewh…
## $ gender <chr> "female", "female", "female", "female", "female", "fema…
## $ weight <dbl> 1740, 1428, 496, 550, 1762, 1004, 522, 1099, 1295, 983
The output shows that q_d2_1 is a character variable, but the values of that variable show three options (Very interested / Somewhat interested / Not at all interested). In this case, we most likely want to change q_d2_1 to be a factor variable and order the factor levels to indicate that this is an ordinal variable. Here is some code on how we might approach this task using the {forcats} package (Wickham 2023):
example_srvy_fct <- example_srvy %>%
mutate(q_d2_1_fct = factor(
q_d2_1,
levels = c(
"Very interested",
"Somewhat interested",
"Not at all interested"
)
))
example_srvy_fct %>%
glimpse()## Rows: 10
## Columns: 7
## $ id <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
## $ region <int> 1, 1, 2, 2, 3, 4, 4, 3, 4, 2
## $ q_d1 <int> 1, 1, NA, 1, 1, NA, NA, 2, 2, 2
## $ q_d2_1 <chr> "Somewhat interested", "Not at all interested", "So…
## $ gender <chr> "female", "female", "female", "female", "female", "…
## $ weight <dbl> 1740, 1428, 496, 550, 1762, 1004, 522, 1099, 1295, …
## $ q_d2_1_fct <fct> Somewhat interested, Not at all interested, Somewha…## # A tibble: 3 × 3
## q_d2_1_fct q_d2_1 n
## <fct> <chr> <int>
## 1 Very interested Very interested 1
## 2 Somewhat interested Somewhat interested 6
## 3 Not at all interested Not at all interested 3
This example dataset also includes a column called region, which is imported as a number (<int>). This is a good reminder to use the questionnaire and codebook along with the data to find out if the values actually reflect a number or are perhaps a coded categorical variable (see Chapter 3 for more details). R calculates the mean even if it is not appropriate, leading to the common mistake of applying an average to categorical values instead of a proportion function. For example, for ease of coding, we may use the across() function to calculate the mean across all numeric variables:
example_des %>%
select(-weight) %>%
summarize(across(where(is.numeric), ~ survey_mean(.x, na.rm = TRUE)))## # A tibble: 1 × 6
## id id_se region region_se q_d1 q_d1_se
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 5.24 1.12 2.49 0.428 1.38 0.196In this example, if we do not adjust region to be a factor variable type, we might accidentally report an average region of 2.49 in our findings, which is meaningless. Checking that our variables are appropriate avoids this pitfall and ensures the measures and models are suitable for the variable type.
12.5 Improve debugging skills
It is common for analysts working in R to come across warning or error messages, and learning how to debug these messages (i.e., find and fix issues) ensures we can proceed with our work and avoid potential mistakes.
We’ve discussed a few examples in this book. For example, if we calculate an average with survey_mean() and get NA instead of a number, it may be because our column has missing values.
## # A tibble: 1 × 2
## mean mean_se
## <dbl> <dbl>
## 1 NA NaNIncluding the na.rm = TRUE would resolve the issue:
## # A tibble: 1 × 2
## mean mean_se
## <dbl> <dbl>
## 1 1.38 0.196
Another common error message that we may see with survey analysis may look something like the following:
## Error in UseMethod("svymean", design): no applicable method for 'svymean' applied to an object of class "formula"
In this case, we need to remember that with functions from the {survey} packages like svyttest(), the design object is not the first argument, and we have to use the dot (.) notation (see Chapter 6). Adding in the named argument of design=. fixes this error.
##
## Design-based t-test
##
## data: q_d1 ~ gender
## t = 3.5, df = 5, p-value = 0.02
## alternative hypothesis: true difference in mean is not equal to 0
## 95 percent confidence interval:
## 0.1878 1.2041
## sample estimates:
## difference in mean
## 0.696Often, debugging involves interpreting the message from R. For example, if our code results in this error:
Error in `contrasts<-`(`*tmp*`, value = contr.funs[1 + isOF[nn]]) :
contrasts can be applied only to factors with 2 or more levelsWe can see that the error has to do with a function requiring a factor with two or more levels and that it has been applied to something else. This ties back to our section on using appropriate variable types. We can check the variable of interest to examine whether it is the correct type.
The internet also offers many resources for debugging. Searching for a specific error message can often lead to a solution. In addition, we can post on community forums like Posit Community for direct help from others.
12.6 Think critically about conclusions
Once we have our findings, we need to learn to think critically about them. As mentioned in Chapter 2, many aspects of the study design can impact our interpretation of the results, for example, the number and types of response options provided to the respondent or who was asked the question (both thinking about the full sample and any skip patterns). Knowing the overall study design can help us accurately think through what the findings may mean and identify any issues with our analyses. Additionally, we should make sure that our survey design object is correctly defined (see Chapter 10), carefully consider how we are managing missing data (see Chapter 11), and follow statistical analysis procedures such as avoiding model overfitting by using too many variables in our formulas.
These considerations allow us to conduct our analyses and review findings for statistically significant results. It is important to note that even significant results do not mean that they are meaningful or important. A large enough sample can produce statistically significant results. Therefore, we want to look at our results in context, such as comparing them with results from other studies or analyzing them in conjunction with confidence intervals and other measures.
Communicating the results (see Chapter 8) in an unbiased manner is also a critical step in any analysis project. If we present results without error measures or only present results that support our initial hypotheses, we are not thinking critically and may incorrectly represent the data. As survey data analysts, we often interpret the survey data for the public. We must ensure that we are the best stewards of the data and work to bring light to meaningful and interesting findings that the public wants and needs to know about.