Chapter 11 Missing data
For this chapter, load the following packages:
library(tidyverse)
library(survey)
library(srvyr)
library(srvyrexploR)
library(naniar)
library(haven)
library(gt)We are using data from ANES and RECS described in Chapter 4. As a reminder, here is the code to create the design objects for each to use throughout this chapter. For ANES, we need to adjust the weight so it sums to the population instead of the sample (see the ANES documentation and Chapter 4 for more information).
targetpop <- 231592693
anes_adjwgt <- anes_2020 %>%
mutate(Weight = Weight / sum(Weight) * targetpop)
anes_des <- anes_adjwgt %>%
as_survey_design(
weights = Weight,
strata = Stratum,
ids = VarUnit,
nest = TRUE
)For RECS, details are included in the RECS documentation and Chapter 10.
11.1 Introduction
Missing data in surveys refer to situations where participants do not provide complete responses to survey questions. Respondents may not have seen a question by design. Or, they may not respond to a question for various other reasons, such as not wanting to answer a particular question, not understanding the question, or simply forgetting to answer. Missing data are important to consider and account for, as they can introduce bias and reduce the representativeness of the data. This chapter provides an overview of the types of missing data, how to assess missing data in surveys, and how to conduct analysis when missing data are present. Understanding this complex topic can help ensure accurate reporting of survey results and provide insight into potential changes to the survey design for the future.
11.2 Missing data mechanisms
There are two main categories that missing data typically fall into: missing by design and unintentional missing data. Missing by design is part of the survey plan and can be more easily incorporated into weights and analyses. Unintentional missing data, on the other hand, can lead to bias in survey estimates if not correctly accounted for. Below we provide more information on the types of missing data.
Missing by design/questionnaire skip logic: This type of missingness occurs when certain respondents are intentionally directed to skip specific questions based on their previous responses or characteristics. For example, in a survey about employment, if a respondent indicates that they are not employed, they may be directed to skip questions related to their job responsibilities. Additionally, some surveys randomize questions or modules so that not all participants respond to all questions. In these instances, respondents would have missing data for the modules not randomly assigned to them.
Unintentional missing data: This type of missingness occurs when researchers do not intend for there to be missing data on a particular question, for example, if respondents did not finish the survey or refused to answer individual questions. There are three main types of unintentional missing data that each should be considered and handled differently (Mack, Su, and Westreich 2018; Schafer and Graham 2002):
Missing completely at random (MCAR): The missing data are unrelated to both observed and unobserved data, and the probability of being missing is the same across all cases. For example, if a respondent missed a question because they had to leave the survey early due to an emergency.
Missing at random (MAR): The missing data are related to observed data but not unobserved data, and the probability of being missing is the same within groups. For example, we know the respondents’ ages and older respondents choose not to answer specific questions but younger respondents do answer them.
Missing not at random (MNAR): The missing data are related to unobserved data, and the probability of being missing varies for reasons we are not measuring. For example, if respondents with depression do not answer a question about depression severity.
11.3 Assessing missing data
Before beginning an analysis, we should explore the data to determine if there is missing data and what types of missing data are present. Conducting descriptive analysis can help with the analysis and reporting of survey data and can inform the survey design in future studies. For example, large amounts of unexpected missing data may indicate the questions were unclear or difficult to recall. There are several ways to explore missing data, which we walk through below. When assessing the missing data, we recommend using a data.frame object and not the survey object, as most of the analysis is about patterns of records, and weights are not necessary.
11.3.1 Summarize data
A very rudimentary first exploration is to use the summary() function to summarize the data, which illuminates NA values in the data. Let’s look at a few analytic variables on the ANES 2020 data using summary():
## V202051 Income7 Income
## Min. :-9.000 $125k or more:1468 Under $9,999 : 647
## 1st Qu.:-1.000 Under $20k :1076 $50,000-59,999 : 485
## Median :-1.000 $20k to < 40k:1051 $100,000-109,999: 451
## Mean :-0.726 $40k to < 60k: 984 $250,000 or more: 405
## 3rd Qu.:-1.000 $60k to < 80k: 920 $80,000-89,999 : 383
## Max. : 3.000 (Other) :1437 (Other) :4565
## NA's : 517 NA's : 517
## V201617x V201616 V201615 V201613 V201611
## Min. :-9.0 Min. :-3 Min. :-3 Min. :-3 Min. :-3
## 1st Qu.: 4.0 1st Qu.:-3 1st Qu.:-3 1st Qu.:-3 1st Qu.:-3
## Median :11.0 Median :-3 Median :-3 Median :-3 Median :-3
## Mean :10.4 Mean :-3 Mean :-3 Mean :-3 Mean :-3
## 3rd Qu.:17.0 3rd Qu.:-3 3rd Qu.:-3 3rd Qu.:-3 3rd Qu.:-3
## Max. :22.0 Max. :-3 Max. :-3 Max. :-3 Max. :-3
##
## V201610 V201607 Gender V201600
## Min. :-3 Min. :-3 Male :3375 Min. :-9.00
## 1st Qu.:-3 1st Qu.:-3 Female:4027 1st Qu.: 1.00
## Median :-3 Median :-3 NA's : 51 Median : 2.00
## Mean :-3 Mean :-3 Mean : 1.47
## 3rd Qu.:-3 3rd Qu.:-3 3rd Qu.: 2.00
## Max. :-3 Max. :-3 Max. : 2.00
##
## RaceEth V201549x V201547z V201547e
## White :5420 Min. :-9.0 Min. :-3 Min. :-3
## Black : 650 1st Qu.: 1.0 1st Qu.:-3 1st Qu.:-3
## Hispanic : 662 Median : 1.0 Median :-3 Median :-3
## Asian, NH/PI : 248 Mean : 1.5 Mean :-3 Mean :-3
## AI/AN : 155 3rd Qu.: 2.0 3rd Qu.:-3 3rd Qu.:-3
## Other/multiple race: 237 Max. : 6.0 Max. :-3 Max. :-3
## NA's : 81
## V201547d V201547c V201547b V201547a V201546
## Min. :-3 Min. :-3 Min. :-3 Min. :-3 Min. :-9.00
## 1st Qu.:-3 1st Qu.:-3 1st Qu.:-3 1st Qu.:-3 1st Qu.: 2.00
## Median :-3 Median :-3 Median :-3 Median :-3 Median : 2.00
## Mean :-3 Mean :-3 Mean :-3 Mean :-3 Mean : 1.84
## 3rd Qu.:-3 3rd Qu.:-3 3rd Qu.:-3 3rd Qu.:-3 3rd Qu.: 2.00
## Max. :-3 Max. :-3 Max. :-3 Max. :-3 Max. : 2.00
##
## Education V201510 AgeGroup Age
## Less than HS: 312 Min. :-9.00 18-29 : 871 Min. :18.0
## High school :1160 1st Qu.: 3.00 30-39 :1241 1st Qu.:37.0
## Post HS :2514 Median : 5.00 40-49 :1081 Median :53.0
## Bachelor's :1877 Mean : 5.62 50-59 :1200 Mean :51.8
## Graduate :1474 3rd Qu.: 6.00 60-69 :1436 3rd Qu.:66.0
## NA's : 116 Max. :95.00 70 or older:1330 Max. :80.0
## NA's : 294 NA's :294
## V201507x TrustPeople V201237
## Min. :-9.0 Always : 48 Min. :-9.00
## 1st Qu.:35.0 Most of the time :3511 1st Qu.: 2.00
## Median :51.0 About half the time:2020 Median : 3.00
## Mean :49.4 Some of the time :1597 Mean : 2.78
## 3rd Qu.:66.0 Never : 264 3rd Qu.: 3.00
## Max. :80.0 NA's : 13 Max. : 5.00
##
## TrustGovernment V201233
## Always : 80 Min. :-9.00
## Most of the time :1016 1st Qu.: 3.00
## About half the time:2313 Median : 4.00
## Some of the time :3313 Mean : 3.43
## Never : 702 3rd Qu.: 4.00
## NA's : 29 Max. : 5.00
##
## PartyID V201231x V201230
## Strong democrat :1796 Min. :-9.00 Min. :-9.000
## Strong republican :1545 1st Qu.: 2.00 1st Qu.:-1.000
## Independent-democrat : 881 Median : 4.00 Median :-1.000
## Independent : 876 Mean : 3.83 Mean : 0.013
## Not very strong democrat: 790 3rd Qu.: 6.00 3rd Qu.: 1.000
## (Other) :1540 Max. : 7.00 Max. : 3.000
## NA's : 25
## V201229 V201228 VotedPres2016_selection
## Min. :-9.000 Min. :-9.00 Clinton:2911
## 1st Qu.:-1.000 1st Qu.: 1.00 Trump :2466
## Median : 1.000 Median : 2.00 Other : 390
## Mean : 0.515 Mean : 1.99 NA's :1686
## 3rd Qu.: 1.000 3rd Qu.: 3.00
## Max. : 2.000 Max. : 5.00
##
## V201103 VotedPres2016 V201102 V201101
## Min. :-9.00 Yes :5810 Min. :-9.000 Min. :-9.000
## 1st Qu.: 1.00 No :1622 1st Qu.:-1.000 1st Qu.:-1.000
## Median : 1.00 NA's: 21 Median : 1.000 Median :-1.000
## Mean : 1.04 Mean : 0.105 Mean : 0.085
## 3rd Qu.: 2.00 3rd Qu.: 1.000 3rd Qu.: 1.000
## Max. : 5.00 Max. : 2.000 Max. : 2.000
##
## V201029 V201028 V201025x V201024
## Min. :-9.000 Min. :-9.0 Min. :-4.00 Min. :-9.00
## 1st Qu.:-1.000 1st Qu.:-1.0 1st Qu.: 3.00 1st Qu.:-1.00
## Median :-1.000 Median :-1.0 Median : 3.00 Median :-1.00
## Mean :-0.897 Mean :-0.9 Mean : 2.92 Mean :-0.86
## 3rd Qu.:-1.000 3rd Qu.:-1.0 3rd Qu.: 3.00 3rd Qu.:-1.00
## Max. :12.000 Max. : 2.0 Max. : 4.00 Max. : 4.00
##
## EarlyVote2020
## Yes : 375
## No : 115
## NA's:6963
##
##
##
## We see that there are NA values in several of the derived variables (those not beginning with “V”) and negative values in the original variables (those beginning with “V”). We can also use the count() function to get an understanding of the different types of missing data on the original variables. For example, let’s look at the count of data for V202072, which corresponds to our VotedPres2020 variable.
## # A tibble: 7 × 3
## VotedPres2020 V202072 n
## <fct> <dbl+lbl> <int>
## 1 Yes -1 [-1. Inapplicable] 361
## 2 Yes 1 [1. Yes, voted for President] 5952
## 3 No -1 [-1. Inapplicable] 10
## 4 No 2 [2. No, didn't vote for President] 77
## 5 <NA> -9 [-9. Refused] 2
## 6 <NA> -6 [-6. No post-election interview] 4
## 7 <NA> -1 [-1. Inapplicable] 1047Here, we can see that there are three types of missing data, and the majority of them fall under the “Inapplicable” category. This is usually a term associated with data missing due to skip patterns and is considered to be missing data by design. Based on the documentation from ANES (DeBell 2010), we can see that this question was only asked to respondents who voted in the election.
11.3.2 Visualization of missing data
It can be challenging to look at tables for every variable and instead may be more efficient to view missing data in a graphical format to help narrow in on patterns or unique variables. The {naniar} package is very useful in exploring missing data visually. We can use the vis_miss() function available in both {visdat} and {naniar} packages to view the amount of missing data by variable (see Figure 11.1) (Tierney 2017; Tierney and Cook 2023).
anes_2020_derived <- anes_2020 %>%
select(
-starts_with("V2"), -CaseID, -InterviewMode,
-Weight, -Stratum, -VarUnit
)
anes_2020_derived %>%
vis_miss(cluster = TRUE, show_perc = FALSE) +
scale_fill_manual(
values = book_colors[c(3, 1)],
labels = c("Present", "Missing"),
name = ""
) +
theme(
plot.margin = margin(5.5, 30, 5.5, 5.5, "pt"),
axis.text.x = element_text(angle = 70)
)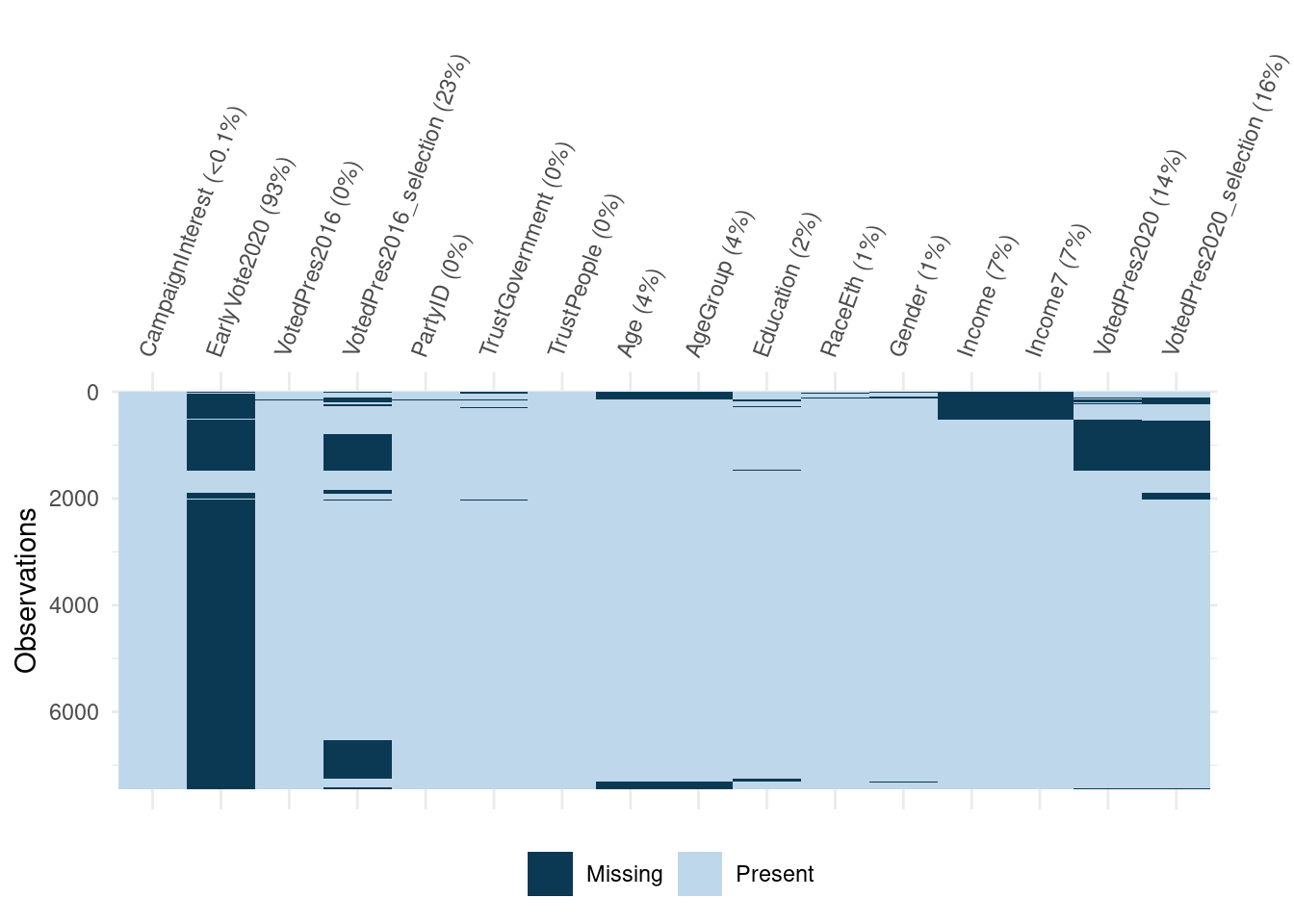
FIGURE 11.1: Visual depiction of missing data in the ANES 2020 data
From the visualization in Figure 11.1, we can start to get a picture of what questions may be connected in terms of missing data. Even if we did not have the informative variable names, we could deduce that VotedPres2020, VotedPres2020_selection, and EarlyVote2020 are likely connected since their missing data patterns are similar.
Additionally, we can also look at VotedPres2016_selection and see that there are a lot of missing data in that variable. The missing data are likely due to a skip pattern, and we can look at other graphics to see how they relate to other variables. The {naniar} package has multiple visualization functions that can help dive deeper, such as the gg_miss_fct() function, which looks at missing data for all variables by levels of another variable (see Figure 11.2).
anes_2020_derived %>%
gg_miss_fct(VotedPres2016) +
scale_fill_gradientn(
guide = "colorbar",
name = "% Miss",
colors = book_colors[c(3, 2, 1)]
) +
ylab("Variable") +
xlab("Voted for President in 2016")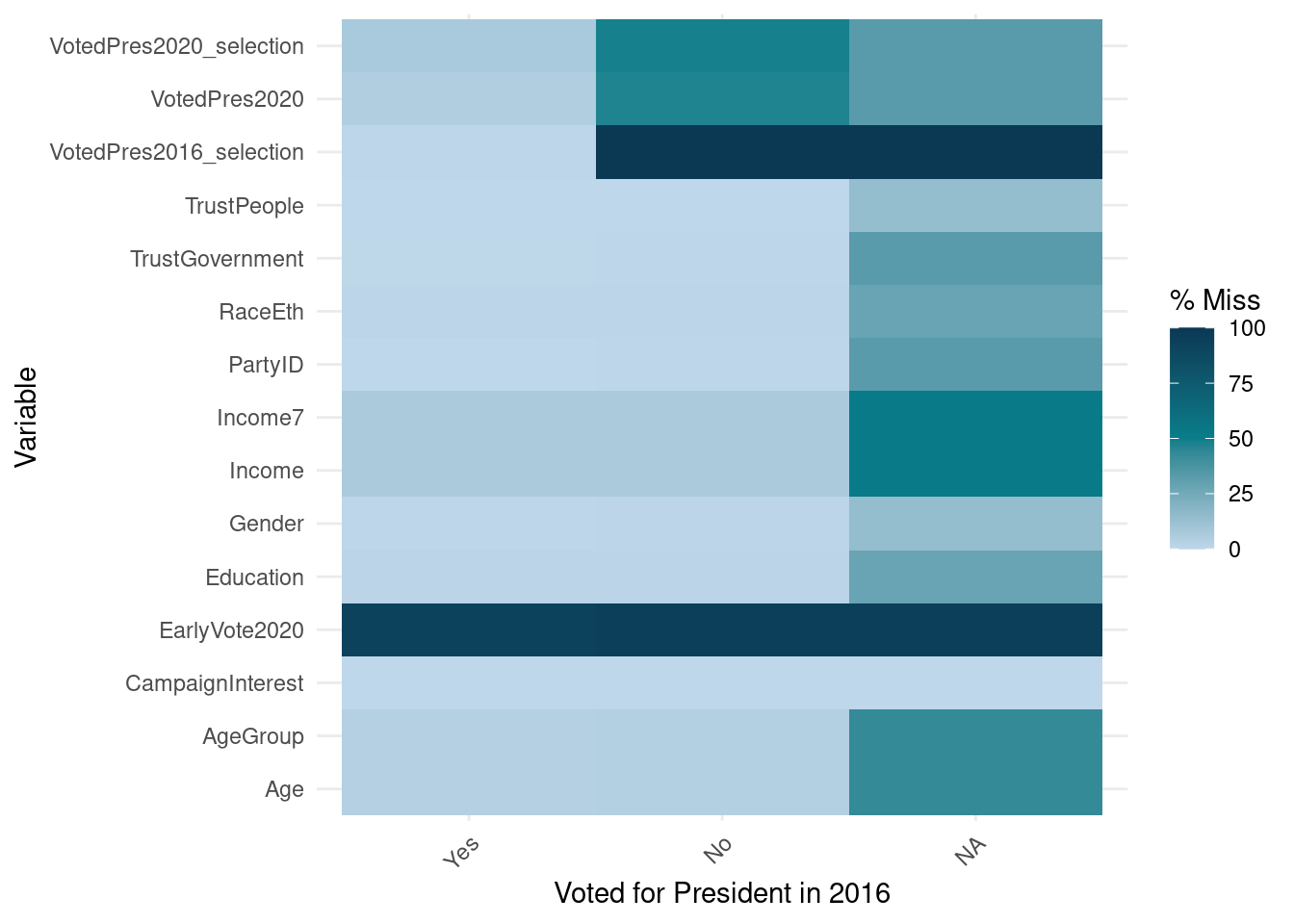
FIGURE 11.2: Missingness in variables for each level of ‘VotedPres2016,’ in the ANES 2020 data
In Figure 11.2, we can see that if respondents did not vote for president in 2016 or did not answer that question, then they were not asked about who they voted for in 2016 (the percentage of missing data is 100%). Additionally, we can see with Figure 11.2 that there are more missing data across all questions if they did not provide an answer to VotedPres2016.
There are other visualizations that work well with numeric data. For example, in the RECS 2020 data, we can plot two continuous variables and the missing data associated with them to see if there are any patterns in the missingness. To do this, we can use the bind_shadow() function from the {naniar} package. This creates a nabular (combination of “na” with “tabular”), which features the original columns followed by the same number of columns with a specific NA format. These NA columns are indicators of whether the value in the original data is missing or not. The example printed below shows how most levels of HeatingBehavior are not missing (!NA) in the NA variable of HeatingBehavior_NA, but those missing in HeatingBehavior are also missing in HeatingBehavior_NA.
## [1] 100## [1] 200## # A tibble: 7 × 3
## HeatingBehavior HeatingBehavior_NA n
## <fct> <fct> <int>
## 1 Set one temp and leave it !NA 7806
## 2 Manually adjust at night/no one home !NA 4654
## 3 Programmable or smart thermostat automatical… !NA 3310
## 4 Turn on or off as needed !NA 1491
## 5 No control !NA 438
## 6 Other !NA 46
## 7 <NA> NA 751We can then use these new variables to plot the missing data alongside the actual data. For example, let’s plot a histogram of the total electric bill grouped by those missing and not missing by heating behavior (see Figure 11.3).
recs_2020_shadow %>%
filter(TOTALDOL < 5000) %>%
ggplot(aes(x = TOTALDOL, fill = HeatingBehavior_NA)) +
geom_histogram() +
scale_fill_manual(
values = book_colors[c(3, 1)],
labels = c("Present", "Missing"),
name = "Heating Behavior"
) +
theme_minimal() +
xlab("Total Energy Cost (Truncated at $5000)") +
ylab("Number of Households")## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.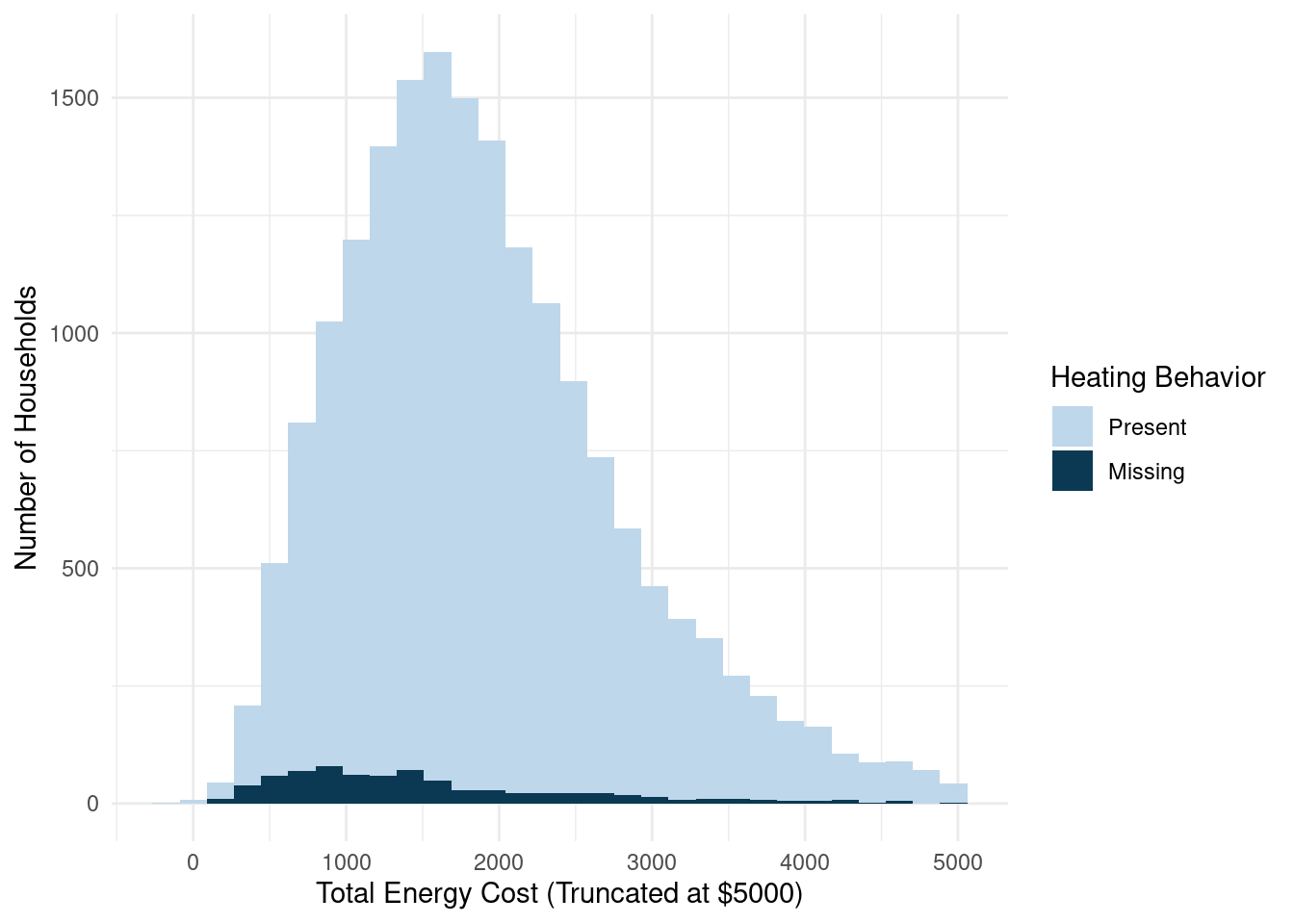
FIGURE 11.3: Histogram of energy cost by heating behavior missing data
Figure 11.3 indicates that respondents who did not provide a response for the heating behavior question may have a different distribution of total energy cost compared to respondents who did provide a response. This view of the raw data and missingness could indicate some bias in the data. Researchers take these different bias aspects into account when calculating weights, and we need to make sure that we incorporate the weights when analyzing the data.
There are many other visualizations that can be helpful in reviewing the data, and we recommend reviewing the {naniar} documentation for more information (Tierney and Cook 2023).
11.4 Analysis with missing data
Once we understand the types of missingness, we can begin the analysis of the data. Different missingness types may be handled in different ways. In most publicly available datasets, researchers have already calculated weights and imputed missing values if necessary. Often, there are imputation flags included in the data that indicate if each value in a given variable is imputed. For example, in the RECS data we may see a logical variable of ZWinterTempNight, where a value of TRUE means that the value of WinterTempNight for that respondent was imputed, and FALSE means that it was not imputed. We may use these imputation flags if we are interested in examining the nonresponse rates in the original data. For those interested in learning more about how to calculate weights and impute data for different missing data mechanisms, we recommend Kim and Shao (2021) and Valliant and Dever (2018).
Even with weights and imputation, missing data are most likely still present and need to be accounted for in analysis. This section provides an overview on how to recode missing data in R, and how to account for skip patterns in analysis.
11.4.1 Recoding missing data
Even within a variable, there can be different reasons for missing data. In publicly released data, negative values are often present to provide different meanings for values. For example, in the ANES 2020 data, they have the following negative values to represent different types of missing data:
- –9: Refused
- –8: Don’t Know
- –7: No post-election data, deleted due to incomplete interview
- –6: No post-election interview
- –5: Interview breakoff (sufficient partial IW)
- –4: Technical error
- –3: Restricted
- –2: Other missing reason (question specific)
- –1: Inapplicable
When we created the derived variables for use in this book, we coded all negative values as NA and proceeded to analyze the data. For most cases, this is an appropriate approach as long as we filter the data appropriately to account for skip patterns (see Section 11.4.2). However, the {naniar} package does have the option to code special missing values. For example, if we wanted to have two NA values, one that indicated the question was missing by design (e.g., due to skip patterns) and one for the other missing categories, we can use the nabular format to incorporate these with the recode_shadow() function.
anes_2020_shadow <- anes_2020 %>%
select(starts_with("V2")) %>%
mutate(across(everything(), ~ case_when(
.x < -1 ~ NA,
TRUE ~ .x
))) %>%
bind_shadow() %>%
recode_shadow(V201103 = .where(V201103 == -1 ~ "skip"))
anes_2020_shadow %>%
count(V201103, V201103_NA)## # A tibble: 5 × 3
## V201103 V201103_NA n
## <dbl+lbl> <fct> <int>
## 1 -1 [-1. Inapplicable] NA_skip 1643
## 2 1 [1. Hillary Clinton] !NA 2911
## 3 2 [2. Donald Trump] !NA 2466
## 4 5 [5. Other {SPECIFY}] !NA 390
## 5 NA NA 43However, it is important to note that at the time of publication, there is no easy way to implement recode_shadow() to multiple variables at once (e.g., we cannot use the tidyverse feature of across()). The example code above only implements this for a single variable, so this would have to be done manually or in a loop for all variables of interest.
11.4.2 Accounting for skip patterns
When questions are skipped by design in a survey, it is meaningful that the data are later missing. For example, the RECS asks people how they control the heat in their home in the winter (HeatingBehavior). This is only among those who have heat in their home (SpaceHeatingUsed). If there is no heating equipment used, the value of HeatingBehavior is missing. One has several choices when analyzing these data which include: (1) only including those with a valid value of HeatingBehavior and specifying the universe as those with heat or (2) including those who do not have heat. It is important to specify what population an analysis generalizes to.
Here is an example where we only include those with a valid value of HeatingBehavior (choice 1). Note that we use the design object (recs_des) and then filter to those that are not missing on HeatingBehavior.
heat_cntl_1 <- recs_des %>%
filter(!is.na(HeatingBehavior)) %>%
group_by(HeatingBehavior) %>%
summarize(
p = survey_prop()
)
heat_cntl_1## # A tibble: 6 × 3
## HeatingBehavior p p_se
## <fct> <dbl> <dbl>
## 1 Set one temp and leave it 0.430 4.69e-3
## 2 Manually adjust at night/no one home 0.264 4.54e-3
## 3 Programmable or smart thermostat automatically adjust… 0.168 3.12e-3
## 4 Turn on or off as needed 0.102 2.89e-3
## 5 No control 0.0333 1.70e-3
## 6 Other 0.00208 3.59e-4Here is an example where we include those who do not have heat (choice 2). To help understand what we are looking at, we have included the output to show both variables, SpaceHeatingUsed and HeatingBehavior.
heat_cntl_2 <- recs_des %>%
group_by(interact(SpaceHeatingUsed, HeatingBehavior)) %>%
summarize(
p = survey_prop()
)
heat_cntl_2## # A tibble: 7 × 4
## SpaceHeatingUsed HeatingBehavior p p_se
## <lgl> <fct> <dbl> <dbl>
## 1 FALSE <NA> 0.0469 2.07e-3
## 2 TRUE Set one temp and leave it 0.410 4.60e-3
## 3 TRUE Manually adjust at night/no one home 0.251 4.36e-3
## 4 TRUE Programmable or smart thermostat aut… 0.160 2.95e-3
## 5 TRUE Turn on or off as needed 0.0976 2.79e-3
## 6 TRUE No control 0.0317 1.62e-3
## 7 TRUE Other 0.00198 3.41e-4
If we ran the first analysis, we would say that 16.8% of households with heat use a programmable or smart thermostat for heating their home. If we used the results from the second analysis, we would say that 16% of households use a programmable or smart thermostat for heating their home. The distinction between the two statements is made bold for emphasis. Skip patterns often change the universe we are talking about and need to be carefully examined.
Filtering to the correct universe is important when handling these types of missing data. The nabular we created above can also help with this. If we have NA_skip values in the shadow, we can make sure that we filter out all of these values and only include relevant missing values. To do this with survey data, we could first create the nabular, then create the design object on that data, and then use the shadow variables to assist with filtering the data. Let’s use the nabular we created above for ANES 2020 (anes_2020_shadow) to create the design object.
anes_adjwgt_shadow <- anes_2020_shadow %>%
mutate(V200010b = V200010b / sum(V200010b) * targetpop)
anes_des_shadow <- anes_adjwgt_shadow %>%
as_survey_design(
weights = V200010b,
strata = V200010d,
ids = V200010c,
nest = TRUE
)Then, we can use this design object to look at the percentage of the population who voted for each candidate in 2016 (V201103). First, let’s look at the percentages without removing any cases:
pres16_select1 <- anes_des_shadow %>%
group_by(V201103) %>%
summarize(
All_Missing = survey_prop()
)
pres16_select1## # A tibble: 5 × 3
## V201103 All_Missing All_Missing_se
## <dbl+lbl> <dbl> <dbl>
## 1 -1 [-1. Inapplicable] 0.324 0.00933
## 2 1 [1. Hillary Clinton] 0.330 0.00728
## 3 2 [2. Donald Trump] 0.299 0.00728
## 4 5 [5. Other {SPECIFY}] 0.0409 0.00230
## 5 NA 0.00627 0.00121Next, we look at the percentages, removing only those missing due to skip patterns (i.e., they did not receive this question).
pres16_select2 <- anes_des_shadow %>%
filter(V201103_NA != "NA_skip") %>%
group_by(V201103) %>%
summarize(
No_Skip_Missing = survey_prop()
)
pres16_select2## # A tibble: 4 × 3
## V201103 No_Skip_Missing No_Skip_Missing_se
## <dbl+lbl> <dbl> <dbl>
## 1 1 [1. Hillary Clinton] 0.488 0.00870
## 2 2 [2. Donald Trump] 0.443 0.00856
## 3 5 [5. Other {SPECIFY}] 0.0606 0.00330
## 4 NA 0.00928 0.00178Finally, we look at the percentages, removing all missing values both due to skip patterns and due to those who refused to answer the question.
pres16_select3 <- anes_des_shadow %>%
filter(V201103_NA == "!NA") %>%
group_by(V201103) %>%
summarize(
No_Missing = survey_prop()
)
pres16_select3## # A tibble: 3 × 3
## V201103 No_Missing No_Missing_se
## <dbl+lbl> <dbl> <dbl>
## 1 1 [1. Hillary Clinton] 0.492 0.00875
## 2 2 [2. Donald Trump] 0.447 0.00861
## 3 5 [5. Other {SPECIFY}] 0.0611 0.00332
| Candidate | Including All Missing Data | Removing Skip Patterns Only | Removing All Missing Data | |||
|---|---|---|---|---|---|---|
| % | s.e. (%) | % | s.e. (%) | % | s.e. (%) | |
| Did Not Vote for President in 2016 | 32.4 | 0.9 | NA | NA | NA | NA |
| Hillary Clinton | 33.0 | 0.7 | 48.8 | 0.9 | 49.2 | 0.9 |
| Donald Trump | 29.9 | 0.7 | 44.3 | 0.9 | 44.7 | 0.9 |
| Other Candidate | 4.1 | 0.2 | 6.1 | 0.3 | 6.1 | 0.3 |
| Missing | 0.6 | 0.1 | 0.9 | 0.2 | NA | NA |
As Table 11.1 shows, the results can vary greatly depending on which type of missing data are removed. If we remove only the skip patterns, the margin between Clinton and Trump is 4.5 percentage points; but if we include all data, even those who did not vote in 2016, the margin is 3.1 percentage points. How we handle the different types of missing values is important for interpreting the data.