Chapter 7 Modeling

Prerequisites

For this chapter, load the following packages:

library(tidyverse)
library(survey)
library(srvyr)
library(srvyrexploR)
library(broom)
library(gt)
library(prettyunits)

We are using data from ANES and RECS described in Chapter 4. As a reminder, here is the code to create the design objects for each to use throughout this chapter. For ANES, we need to adjust the weight so it sums to the population instead of the sample (see the ANES documentation and Chapter 4 for more information).

targetpop <- 231592693

anes_adjwgt <- anes_2020 %>%
  mutate(Weight = Weight / sum(Weight) * targetpop)

anes_des <- anes_adjwgt %>%
  as_survey_design(
    weights = Weight,
    strata = Stratum,
    ids = VarUnit,
    nest = TRUE
  )

For RECS, details are included in the RECS documentation and Chapters 4 and 10.

recs_des <- recs_2020 %>%
  as_survey_rep(
    weights = NWEIGHT,
    repweights = NWEIGHT1:NWEIGHT60,
    type = "JK1",
    scale = 59 / 60,
    mse = TRUE
  )

7.1 Introduction

Modeling data is a way for researchers to investigate the relationship between a single dependent variable and one or more independent variables. This builds upon the analyses conducted in Chapter 6, which looked at the relationships between just two variables. For example, in Example 3 in Section 6.3.2, we investigated if there is a relationship between the electrical bill cost and whether or not the household used air conditioning (A/C). However, there are potentially other elements that could go into what the cost of electrical bills are in a household (e.g., outside temperature, desired internal temperature, types and number of appliances, etc.).

T-tests only allow us to investigate the relationship of one independent variable at a time, but using models, we can look into multiple variables and even explore interactions between these variables. There are several types of models, but in this chapter, we cover Analysis of Variance (ANOVA) and linear regression models following common normal (Gaussian) and logit models. Jonas Kristoffer Lindeløv has an interesting discussion of many statistical tests and models being equivalent to a linear model. For example, a one-way ANOVA is a linear model with one categorical independent variable, and a two-sample t-test is an ANOVA where the independent variable has exactly two levels.

When modeling data, it is helpful to first create an equation that provides an overview of what we are modeling. The main structure of these models is as follows:

\[y_i=\beta_0 +\sum_{i=1}^p \beta_i x_i + \epsilon_i\]

where $y_i$ is the outcome, $\beta_0$ is an intercept, $x_1, \cdots, x_p$ are the predictors with $\beta_1, \cdots, \beta_p$ as the associated coefficients, and $\epsilon_i$ is the error. Not all models have all components. For example, some models may not include an intercept ($\beta_0$), may have interactions between different independent variables ($x_i$), or may have different underlying structures for the dependent variable ($y_i$). However, all linear models have the independent variables related to the dependent variable in a linear form.

To specify these models in R, the formulas are the same with both survey data and other data. The left side of the formula is the response/dependent variable, and the right side has the predictor/independent variable(s). There are many symbols used in R to specify the formula.

For example, a linear formula mathematically notated as

\[y_i=\beta_0+\beta_1 x_i+\epsilon_i\] would be specified in R as y~x where the intercept is not explicitly included. To fit a model with no intercept, that is,

\[y_i=\beta_1 x_i+\epsilon_i\] it can be specified in R as y~x-1. Formula notation details in R can be found in the help file for formula²¹. A quick overview of the common formula notation is in Table 7.1:

TABLE 7.1: Common symbols in formula notation
Symbol	Example	Meaning
+	`+x`	include this variable
-	`-x`	delete this variable
:	`x:z`	include the interaction between these variables
*	`x*z`	include these variables and the interactions between them
`^n`	`(x+y+z)^3`	include these variables and all interactions up to n-way
I	`I(x-z)`	as-is: include a new variable that is calculated inside the parentheses (e.g., x-z, x*z, x/z are possible calculations that could be done)

There are often multiple ways to specify the same formula. For example, consider the following equation using the mtcars dataset that is built into R:

\[mpg_i=\beta_0+\beta_1cyl_{i}+\beta_2disp_{i}+\beta_3hp_{i}+\beta_4cyl_{i}disp_{i}+\beta_5cyl_{i}hp_{i}+\beta_6disp_{i}hp_{i}+\epsilon_i\]

This could be specified in R code as any of the following:

mpg ~ (cyl + disp + hp)^2
mpg ~ cyl + disp + hp + cyl:disp + cyl:hp + disp:hp
mpg ~ cyl*disp + cyl*hp + disp*hp

In the above options, the ways the : and * notations are implemented are different. Using : only includes the interactions and not the main effects, while using * includes the main effects and all possible interactions. Table 7.2 provides an overview of the syntax and differences between the two notations.

TABLE 7.2: Differences in formulas for `:` and `*` code syntax
Symbol	Syntax	Formula
:	`mpg ~ cyl:disp:hp`	\[ \begin{aligned} mpg_i = &\beta_0+\beta_4cyl_{i}disp_{i}+\beta_5cyl_{i}hp_{i}+ \\& \beta_6disp_{i}hp_{i}+\epsilon_i\end{aligned}\]
*	`mpg ~ cyldisphp`	\[ \begin{aligned} mpg_i= &\beta_0+\beta_1cyl_{i}+\beta_2disp_{i}+\beta_3hp_{i}+\\& \beta_4cyl_{i}disp_{i}+\beta_5cyl_{i}hp_{i}+\beta_6disp_{i}hp_{i}+\\&\beta_7cyl_{i}disp_{i}hp_{i}+\epsilon_i\end{aligned}\]

When using non-survey data, such as experimental or observational data, researchers use the glm() function for linear models. With survey data, however, we use svyglm() from the {survey} package to ensure that we account for the survey design and weights in modeling²². This allows us to generalize a model to the population of interest and accounts for the fact that the observations in the survey data may not be independent. As discussed in Chapter 6, modeling survey data cannot be directly done in {srvyr}, but can be done in the {survey} package (Lumley 2010). In this chapter, we provide syntax and examples for linear models, including ANOVA, normal linear regression, and logistic regression. For details on other types of regression, including ordinal regression, log-linear models, and survival analysis, refer to Lumley (2010). Lumley (2010) also discusses custom models such as a negative binomial or Poisson model in appendix E of his book.

7.2 Analysis of variance

In ANOVA, we are testing whether the mean of an outcome is the same across two or more groups. Statistically, we set up this as follows:

$H_0: \mu_1 = \mu_2= \dots = \mu_k$ where $\mu_i$ is the mean outcome for group $i$
$H_A: \text{At least one mean is different}$

An ANOVA test is also a linear model, we can re-frame the problem using the framework as:

\[ y_i=\sum_{i=1}^k \mu_i x_i + \epsilon_i\]

where $x_i$ is a group indicator for groups $1, \cdots, k$.

Some assumptions when using ANOVA on survey data include:

The outcome variable is normally distributed within each group.
The variances of the outcome variable between each group are approximately equal.
We do NOT assume independence between the groups as with ANOVA on non-survey data. The covariance is accounted for in the survey design.

7.2.1 Syntax

To perform this type of analysis in R, the general syntax is as follows:

des_obj %>%
  svyglm(
    formula = outcome ~ group,
    design = .,
    na.action = na.omit,
    df.resid = NULL
  )

The arguments are:

formula: formula in the form of outcome~group. The group variable must be a factor or character.
design: a tbl_svy object created by as_survey
na.action: handling of missing data
df.resid: degrees of freedom for Wald tests (optional); defaults to using degf(design)-(g-1) where $g$ is the number of groups

The function svyglm() does not have the design as the first argument so the dot (.) notation is used to pass it with a pipe (see Chapter 6 for more details). The default for missing data is na.omit. This means that we are removing all records with any missing data in either predictors or outcomes from analyses. There are other options for handling missing data, and we recommend looking at the help documentation for na.omit (run help(na.omit) or ?na.omit) for more information on options to use for na.action. For a discussion on how to handle missing data, see Chapter 11.

7.2.2 Example

Looking at an example helps us discuss the output and how to interpret the results. In RECS, respondents are asked what temperature they set their thermostat to during the evening when using A/C during the summer²³. To analyze these data, we filter the respondents to only those using A/C (ACUsed)²⁴. Then, if we want to see if there are regional differences, we can use group_by(). A descriptive analysis of the temperature at night (SummerTempNight) set by region and the sample sizes is displayed below.

recs_des %>%
  filter(ACUsed) %>%
  group_by(Region) %>%
  summarize(
    SMN = survey_mean(SummerTempNight, na.rm = TRUE),
    n = unweighted(n()),
    n_na = unweighted(sum(is.na(SummerTempNight)))
  )

## # A tibble: 4 × 5
##   Region      SMN SMN_se     n  n_na
##   <fct>     <dbl>  <dbl> <int> <int>
## 1 Northeast  69.7 0.103   3204     0
## 2 Midwest    71.0 0.0897  3619     0
## 3 South      71.8 0.0536  6065     0
## 4 West       72.5 0.129   3283     0

In the following code, we test whether this temperature varies by region by first using svyglm() to run the test and then using broom::tidy() to display the output. Note that the temperature setting is set to NA when the household does not use A/C, and since the default handling of NAs is na.action=na.omit, records that do not use A/C are not included in this regression.

anova_out <- recs_des %>%
  svyglm(
    design = .,
    formula = SummerTempNight ~ Region
  )

tidy(anova_out)

## # A tibble: 4 × 5
##   term          estimate std.error statistic   p.value
##   <chr>            <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept)      69.7      0.103    674.   3.69e-111
## 2 RegionMidwest     1.34     0.138      9.68 1.46e- 13
## 3 RegionSouth       2.05     0.128     16.0  1.36e- 22
## 4 RegionWest        2.80     0.177     15.9  2.27e- 22

In the output above, we can see the estimated coefficients (estimate), estimated standard errors of the coefficients (std.error), the t-statistic (statistic), and the p-value for each coefficient. In this output, the intercept represents the reference value of the Northeast region. The other coefficients indicate the difference in temperature relative to the Northeast region. For example, in the Midwest, temperatures are set, on average, 1.34 (p-value is <0.0001) degrees higher than in the Northeast during summer nights, and each region sets its thermostats at significantly higher temperatures than the Northeast.

If we wanted to change the reference value, we would reorder the factor before modeling using the relevel() function from {stats} or using one of many factor ordering functions in {forcats} such as fct_relevel() or fct_infreq(). For example, if we wanted the reference level to be the Midwest region, we could use the following code with the results in Table 7.3. Note the usage of the gt() function on top of tidy() to print a nice-looking output table (Iannone et al. 2024; Robinson, Hayes, and Couch 2023) (see Chapter 8 for more information on the {gt} package).

anova_out_relevel <- recs_des %>%
  mutate(Region = fct_relevel(Region, "Midwest", after = 0)) %>%
  svyglm(
    design = .,
    formula = SummerTempNight ~ Region
  )

tidy(anova_out_relevel) %>%
  mutate(p.value = pretty_p_value(p.value)) %>%
  gt() %>%
  fmt_number()

TABLE 7.3: ANOVA output for estimates of thermostat temperature setting at night by region with Midwest as the reference region, RECS 2020
term	estimate	std.error	statistic	p.value
(Intercept)	71.04	0.09	791.83	<0.0001
RegionNortheast	−1.34	0.14	−9.68	<0.0001
RegionSouth	0.71	0.10	6.91	<0.0001
RegionWest	1.47	0.16	9.17	<0.0001

This output now has the coefficients indicating the difference in temperature relative to the Midwest region. For example, in the Northeast, temperatures are set, on average, 1.34 (p-value is <0.0001) degrees lower than in the Midwest during summer nights, and each region sets its thermostats at significantly lower temperatures than the Midwest. This is the reverse of what we saw in the prior model, as we are still comparing the same two regions, just from different reference points.

7.3 Normal linear regression

Normal linear regression is a more generalized method than ANOVA, where we fit a model of a continuous outcome with any number of categorical or continuous predictors (whereas ANOVA only has categorical predictors) and is similarly specified as:

\[\begin{equation} y_i=\beta_0 +\sum_{i=1}^p \beta_i x_i + \epsilon_i \end{equation}\]

where $y_i$ is the outcome, $\beta_0$ is an intercept, $x_1, \cdots, x_p$ are the predictors with $\beta_1, \cdots, \beta_p$ as the associated coefficients, and $\epsilon_i$ is the error.

Assumptions in normal linear regression using survey data include:

The residuals ($\epsilon_i$) are normally distributed, but there is not an assumption of independence, and the correlation structure is captured in the survey design object
There is a linear relationship between the outcome variable and the independent variables
The residuals are homoscedastic; that is, the error term is the same across all values of independent variables

7.3.1 Syntax

The syntax for this regression uses the same function as ANOVA but can have more than one variable listed on the right-hand side of the formula:

des_obj %>%
  svyglm(
    formula = outcomevar ~ x1 + x2 + x3,
    design = .,
    na.action = na.omit,
    df.resid = NULL
  )

The arguments are:

formula: formula in the form of y~x
design: a tbl_svy object created by as_survey
na.action: handling of missing data
df.resid: degrees of freedom for Wald tests (optional); defaults to using degf(design)-p where $p$ is the rank of the design matrix

As discussed in Section 7.1, the formula on the right-hand side can be specified in many ways, for example, denoting whether or not interactions are desired.

7.3.2 Examples

Example 1: Linear regression with a single variable

On RECS, we can obtain information on the square footage of homes²⁵ and the electric bills. We assume that square footage is related to the amount of money spent on electricity and examine a model for this. Before any modeling, we first plot the data to determine whether it is reasonable to assume a linear relationship. In Figure 7.1, each hexagon represents the weighted count of households in the bin, and we can see a general positive linear trend (as the square footage increases, so does the amount of money spent on electricity).

recs_2020 %>%
  ggplot(aes(
    x = TOTSQFT_EN,
    y = DOLLAREL,
    weight = NWEIGHT / 1000000
  )) +
  geom_hex() +
  scale_fill_gradientn(
    guide = "colorbar",
    name = "Housing Units\n(Millions)",
    labels = scales::comma,
    colors = book_colors[c(3, 2, 1)]
  ) +
  xlab("Total square footage") +
  ylab("Amount spent on electricity") +
  scale_y_continuous(labels = scales::dollar_format()) +
  scale_x_continuous(labels = scales::comma_format()) +
  theme_minimal()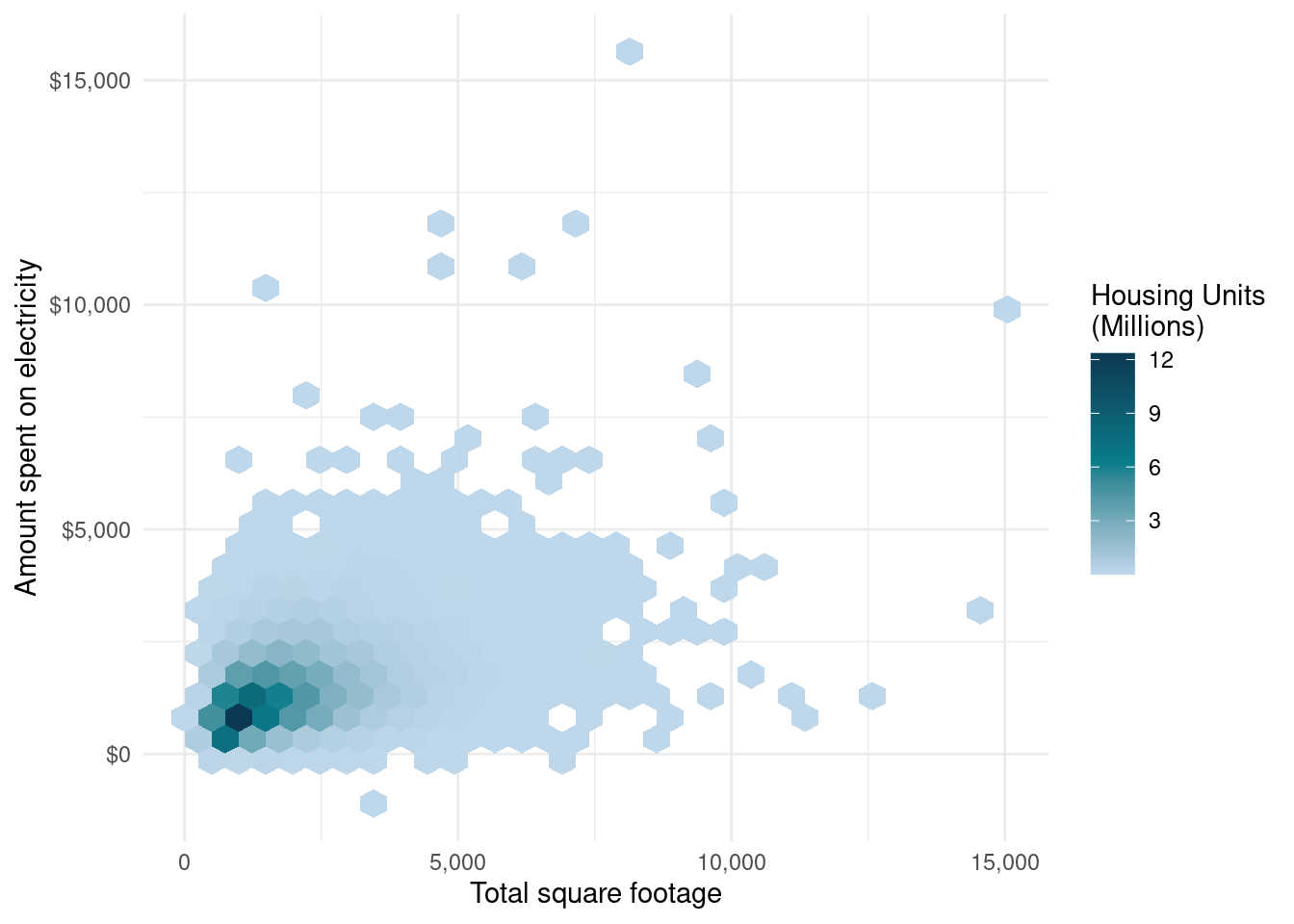

Hex chart where each hexagon represents a number of housing units at a point. x-axis is 'Total square footage' ranging from 0 to 7,500 and y-axis is 'Amount spent on electricity' ranging from $0 to 8,000. The trend is relatively linear and positive. A high concentration of points have square footage between 0 and 2,500 square feet as well as between electricity expenditure between $0 and 2,000

FIGURE 7.1: Relationship between square footage and dollars spent on electricity, RECS 2020

Given that the plot shows a potentially increasing relationship between square footage and electricity expenditure, fitting a model allows us to determine if the relationship is statistically significant. The model is fit below with electricity expenditure as the outcome.

m_electric_sqft <- recs_des %>%
  svyglm(
    design = .,
    formula = DOLLAREL ~ TOTSQFT_EN,
    na.action = na.omit
  )

tidy(m_electric_sqft) %>%
  mutate(p.value = pretty_p_value(p.value)) %>%
  gt() %>%
  fmt_number()

TABLE 7.4: Linear regression output predicting electricity expenditure given square footage, RECS 2020
term	estimate	std.error	statistic	p.value
(Intercept)	836.72	12.77	65.51	<0.0001
TOTSQFT_EN	0.30	0.01	41.67	<0.0001

In Table 7.4, we can see the estimated coefficients (estimate), estimated standard errors of the coefficients (std.error), the t-statistic (statistic), and the p-value for each coefficient. In these results, we can say that, on average, for every additional square foot of house size, the electricity bill increases by 30 cents, and that square footage is significantly associated with electricity expenditure (p-value is <0.0001).

This is a straightforward model, and there are likely many more factors related to electricity expenditure, including the type of cooling, number of appliances, location, and more. However, starting with one-variable models can help analysts understand what potential relationships there are between variables before fitting more complex models. Often, we start with known relationships before building models to determine what impact additional variables have on the model.

Example 2: Linear regression with multiple variables and interactions

In the following example, a model is fit to predict electricity expenditure, including census region (factor/categorical), urbanicity (factor/categorical), square footage (double/numeric), and whether A/C is used (logical/categorical) with all two-way interactions also included. In this example, we are choosing to fit this model without an intercept (using -1 in the formula). This results in an intercept estimate for each region instead of a single intercept for all data.

m_electric_multi <- recs_des %>%
  svyglm(
    design = .,
    formula =
      DOLLAREL ~ (Region + Urbanicity + TOTSQFT_EN + ACUsed)^2 - 1,
    na.action = na.omit
  )

tidy(m_electric_multi) %>%
  mutate(p.value = pretty_p_value(p.value)) %>%
  gt() %>%
  fmt_number()

TABLE 7.5: Linear regression output predicting electricity expenditure given region, urbanicity, square footage, A/C usage, and one-way interactions, RECS 2020
term	estimate	std.error	statistic	p.value
RegionNortheast	543.73	56.57	9.61	<0.0001
RegionMidwest	702.16	78.12	8.99	<0.0001
RegionSouth	938.74	46.99	19.98	<0.0001
RegionWest	603.27	36.31	16.61	<0.0001
UrbanicityUrban Cluster	73.03	81.50	0.90	0.3764
UrbanicityRural	204.13	80.69	2.53	0.0161
TOTSQFT_EN	0.24	0.03	8.65	<0.0001
ACUsedTRUE	252.06	54.05	4.66	<0.0001
RegionMidwest:UrbanicityUrban Cluster	183.06	82.38	2.22	0.0328
RegionSouth:UrbanicityUrban Cluster	152.56	76.03	2.01	0.0526
RegionWest:UrbanicityUrban Cluster	98.02	75.16	1.30	0.2007
RegionMidwest:UrbanicityRural	312.83	50.88	6.15	<0.0001
RegionSouth:UrbanicityRural	220.00	55.00	4.00	0.0003
RegionWest:UrbanicityRural	180.97	58.70	3.08	0.0040
RegionMidwest:TOTSQFT_EN	−0.05	0.02	−2.09	0.0441
RegionSouth:TOTSQFT_EN	0.00	0.03	0.11	0.9109
RegionWest:TOTSQFT_EN	−0.03	0.03	−1.00	0.3254
RegionMidwest:ACUsedTRUE	−292.97	60.24	−4.86	<0.0001
RegionSouth:ACUsedTRUE	−294.07	57.44	−5.12	<0.0001
RegionWest:ACUsedTRUE	−77.68	47.05	−1.65	0.1076
UrbanicityUrban Cluster:TOTSQFT_EN	−0.04	0.02	−1.63	0.1112
UrbanicityRural:TOTSQFT_EN	−0.06	0.02	−2.60	0.0137
UrbanicityUrban Cluster:ACUsedTRUE	−130.23	60.30	−2.16	0.0377
UrbanicityRural:ACUsedTRUE	−33.80	59.30	−0.57	0.5724
TOTSQFT_EN:ACUsedTRUE	0.08	0.02	3.48	0.0014

As shown in Table 7.5, there are many terms in this model. To test whether coefficients for a term are different from zero, the regTermTest() function can be used. For example, in the above regression, we can test whether the interaction of region and urbanicity is significant as follows:

urb_reg_test <- regTermTest(m_electric_multi, ~ Urbanicity:Region)
urb_reg_test

## Wald test for Urbanicity:Region
##  in svyglm(design = ., formula = DOLLAREL ~ (Region + Urbanicity + 
##     TOTSQFT_EN + ACUsed)^2 - 1, na.action = na.omit)
## F =  6.851  on  6  and  35  df: p= 7.2e-05

This output indicates there is a significant interaction between urbanicity and region (p-value is <0.0001).

To examine the predictions, residuals, and more from the model, the augment() function from {broom} can be used. The augment() function returns a tibble with the independent and dependent variables and other fit statistics. The augment() function has not been specifically written for objects of class svyglm, and as such, a warning is displayed indicating this at this time. As it was not written exactly for this class of objects, a little tweaking needs to be done after using augment(). To obtain the standard error of the predicted values (.se.fit), we need to use the attr() function on the predicted values (.fitted) created by augment(). Additionally, the predicted values created are outputted with a type of svrep. If we want to plot the predicted values, we need to use as.numeric() to get the predicted values into a numeric format to work with. However, it is important to note that this adjustment must be completed after the standard error adjustment.

fitstats <-
  augment(m_electric_multi) %>%
  mutate(
    .se.fit = sqrt(attr(.fitted, "var")),
    .fitted = as.numeric(.fitted)
  )

fitstats

## # A tibble: 18,496 × 13
##    DOLLAREL Region    Urbanicity   TOTSQFT_EN ACUsed `(weights)` .fitted
##       <dbl> <fct>     <fct>             <dbl> <lgl>        <dbl>   <dbl>
##  1    1955. West      Urban Area         2100 TRUE         0.492   1397.
##  2     713. South     Urban Area          590 TRUE         1.35    1090.
##  3     335. West      Urban Area          900 TRUE         0.849   1043.
##  4    1425. South     Urban Area         2100 TRUE         0.793   1584.
##  5    1087  Northeast Urban Area          800 TRUE         1.49    1055.
##  6    1896. South     Urban Area         4520 TRUE         1.09    2375.
##  7    1418. South     Urban Area         2100 TRUE         0.851   1584.
##  8    1237. South     Urban Clust…        900 FALSE        1.45    1349.
##  9     538. South     Urban Area          750 TRUE         0.185   1142.
## 10     625. West      Urban Area          760 TRUE         1.06    1002.
## # ℹ 18,486 more rows
## # ℹ 6 more variables: .resid <dbl>, .hat <dbl>, .sigma <dbl>,
## #   .cooksd <dbl>, .std.resid <dbl>, .se.fit <dbl>

These results can then be used in a variety of ways, including examining residual plots as illustrated in the code below and Figure 7.2. In the residual plot, we look for any patterns in the data. If we do see patterns, this may indicate a violation of the heteroscedasticity assumption and the standard errors of the coefficients may be incorrect. In Figure 7.2, we do not see a strong pattern indicating that our assumption of heteroscedasticity may hold.

fitstats %>%
  ggplot(aes(x = .fitted, .resid)) +
  geom_point(alpha = .1) +
  geom_hline(yintercept = 0, color = "red") +
  theme_minimal() +
  xlab("Fitted value of electricity cost") +
  ylab("Residual of model") +
  scale_y_continuous(labels = scales::dollar_format()) +
  scale_x_continuous(labels = scales::dollar_format())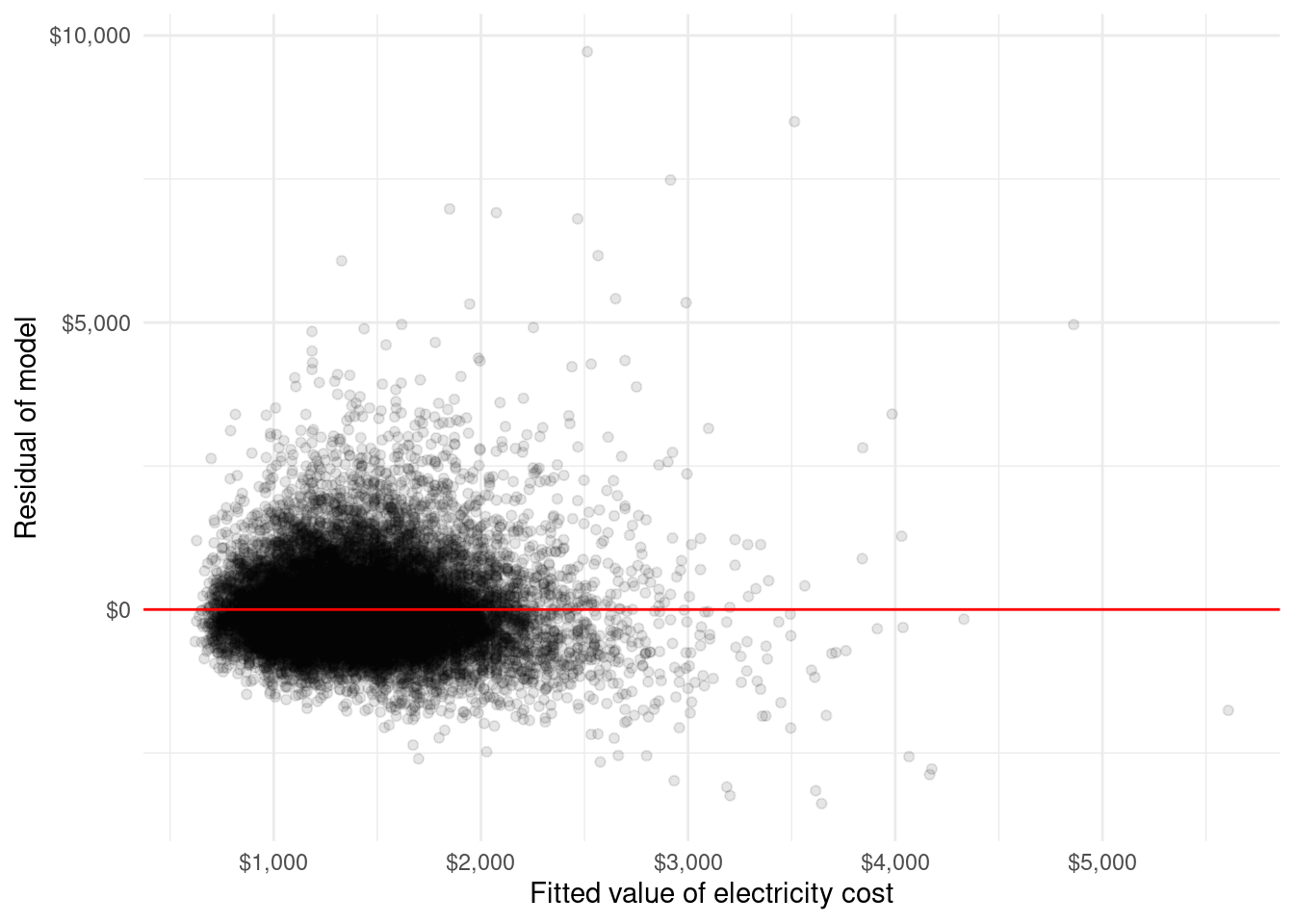

Residual scatter plot with a x-axis of 'Fitted value of electricity cost' ranging between approximately $0 and $4,000 and a y-axis with the 'Residual of model' ranging from approximately -$3,000 to $5,000. The points create a slight megaphone shape with largest residuals in the middle of the x-range. A red line is drawn horizontally at y=0.

FIGURE 7.2: Residual plot of electric cost model with the following covariates: Region, Urbanicity, TOTSQFT_EN, and ACUsed

Additionally, augment() can be used to predict outcomes for data not used in modeling. Perhaps we would like to predict the energy expenditure for a home in an urban area in the south that uses A/C and is 2,500 square feet. To do this, we first make a tibble including that additional data and then use the newdata argument in the augment() function. As before, to obtain the standard error of the predicted values, we need to use the attr() function.

add_data <- recs_2020 %>%
  select(
    DOEID, Region, Urbanicity,
    TOTSQFT_EN, ACUsed,
    DOLLAREL
  ) %>%
  rbind(
    tibble(
      DOEID = NA,
      Region = "South",
      Urbanicity = "Urban Area",
      TOTSQFT_EN = 2500,
      ACUsed = TRUE,
      DOLLAREL = NA
    )
  ) %>%
  tail(1)

pred_data <- augment(m_electric_multi, newdata = add_data) %>%
  mutate(
    .se.fit = sqrt(attr(.fitted, "var")),
    .fitted = as.numeric(.fitted)
  )

pred_data

## # A tibble: 1 × 8
##   DOEID Region Urbanicity TOTSQFT_EN ACUsed DOLLAREL .fitted .se.fit
##   <dbl> <fct>  <fct>           <dbl> <lgl>     <dbl>   <dbl>   <dbl>
## 1    NA South  Urban Area       2500 TRUE         NA   1715.    22.6

In the above example, it is predicted that the energy expenditure would be $1,715.

7.4 Logistic regression

Logistic regression is used to model binary outcomes, such as whether or not someone voted. There are several instances where an outcome may not be originally binary but is collapsed into being binary. For example, given that gender is often asked in surveys with multiple response options and not a binary scale, many researchers now code gender in logistic modeling as “cis-male” compared to not “cis-male.” We could also convert a 4-point Likert scale that has levels of “Strongly Agree,” “Agree,” “Disagree,” and “Strongly Disagree” to group the agreement levels into one group and disagreement levels into a second group.

Logistic regression is a specific case of the generalized linear model (GLM). A GLM uses a link function to link the response variable to the linear model. If we tried to use a normal linear regression with a binary outcome, many assumptions would not hold, namely, the response would not be continuous. Logistic regression allows us to link a linear model between the covariates and the propensity of an outcome. In logistic regression, the link model is the logit function. Specifically, the model is specified as follows:

\[ y_i \sim \text{Bernoulli}(\pi_i)\]

\[\begin{equation} \log \left(\frac{\pi_i}{1-\pi_i} \right)=\beta_0 +\sum_{i=1}^n \beta_i x_i \end{equation}\]

which can be re-expressed as

\[ \pi_i=\frac{\exp \left(\beta_0 +\sum_{i=1}^n \beta_i x_i \right)}{1+\exp \left(\beta_0 +\sum_{i=1}^n \beta_i x_i \right)}\] where $y_i$ is the outcome, $\beta_0$ is an intercept, and $x_1, \cdots, x_n$ are the predictors with $\beta_1, \cdots, \beta_n$ as the associated coefficients.

The Bernoulli distribution is a distribution which has an outcome of 0 or 1 given some probability ($\pi_i$) in this case, and we model $\pi_i$ as a function of the covariates $x_i$ using this logit link.

Assumptions in logistic regression using survey data include:

The outcome variable has two levels
There is a linear relationship between the independent variables and the log odds (the equation for the logit function)
The residuals are homoscedastic; that is, the error term is the same across all values of independent variables

7.4.1 Syntax

The syntax for logistic regression is as follows:

des_obj %>%
  svyglm(
    formula = outcomevar ~ x1 + x2 + x3,
    design = .,
    na.action = na.omit,
    df.resid = NULL,
    family = quasibinomial
  )

The arguments are:

formula: Formula in the form of y~x
design: a tbl_svy object created by as_survey
na.action: handling of missing data
df.resid: degrees of freedom for Wald tests (optional); defaults to using degf(design)-p where $p$ is the rank of the design matrix
family: the error distribution/link function to be used in the model

Note svyglm() is the same function used in both ANOVA and normal linear regression. However, we’ve added the link function quasibinomial. While we can use the binomial link function, it is recommended to use the quasibinomial as our weights may not be integers, and the quasibinomial also allows for overdispersion (Lumley 2010; McCullagh and Nelder 1989; R Core Team 2024). The quasibinomial family has a default logit link, which is specified in the equations above. When specifying the outcome variable, it is likely specified in one of three ways with survey data:

A two-level factor variable where the first level of the factor indicates a “failure,” and the second level indicates a “success”
A numeric variable which is 1 or 0 where 1 indicates a success
A logical variable where TRUE indicates a success

7.4.2 Examples

Example 1: Logistic regression with single variable

In the following example, we use the ANES data to model whether someone usually has trust in the government²⁶ by whom someone voted for president in 2020. As a reminder, the leading candidates were Biden and Trump, though people could vote for someone else not in the Democratic or Republican parties. Those votes are all grouped into an “Other” category. We first create a binary outcome for trusting in the government by collapsing “Always” and “Most of the time” into a single-factor level, and the other response options (“About half the time,” “Some of the time,” and “Never”) into a second factor level. Next, a scatter plot of the raw data is not useful, as it is all 0 and 1 outcomes; so instead, we plot a summary of the data.

anes_des_der <- anes_des %>%
  mutate(TrustGovernmentUsually = case_when(
    is.na(TrustGovernment) ~ NA,
    TRUE ~ TrustGovernment %in% c("Always", "Most of the time")
  ))

anes_des_der %>%
  group_by(VotedPres2020_selection) %>%
  summarize(
    pct_trust = survey_mean(TrustGovernmentUsually,
      na.rm = TRUE,
      proportion = TRUE,
      vartype = "ci"
    ),
    .groups = "drop"
  ) %>%
  filter(complete.cases(.)) %>%
  ggplot(aes(
    x = VotedPres2020_selection, y = pct_trust,
    fill = VotedPres2020_selection
  )) +
  geom_bar(stat = "identity") +
  geom_errorbar(aes(ymin = pct_trust_low, ymax = pct_trust_upp),
    width = .2
  ) +
  scale_fill_manual(values = c("#0b3954", "#bfd7ea", "#8d6b94")) +
  xlab("Election choice (2020)") +
  ylab("Usually trust the government") +
  scale_y_continuous(labels = scales::percent) +
  guides(fill = "none") +
  theme_minimal()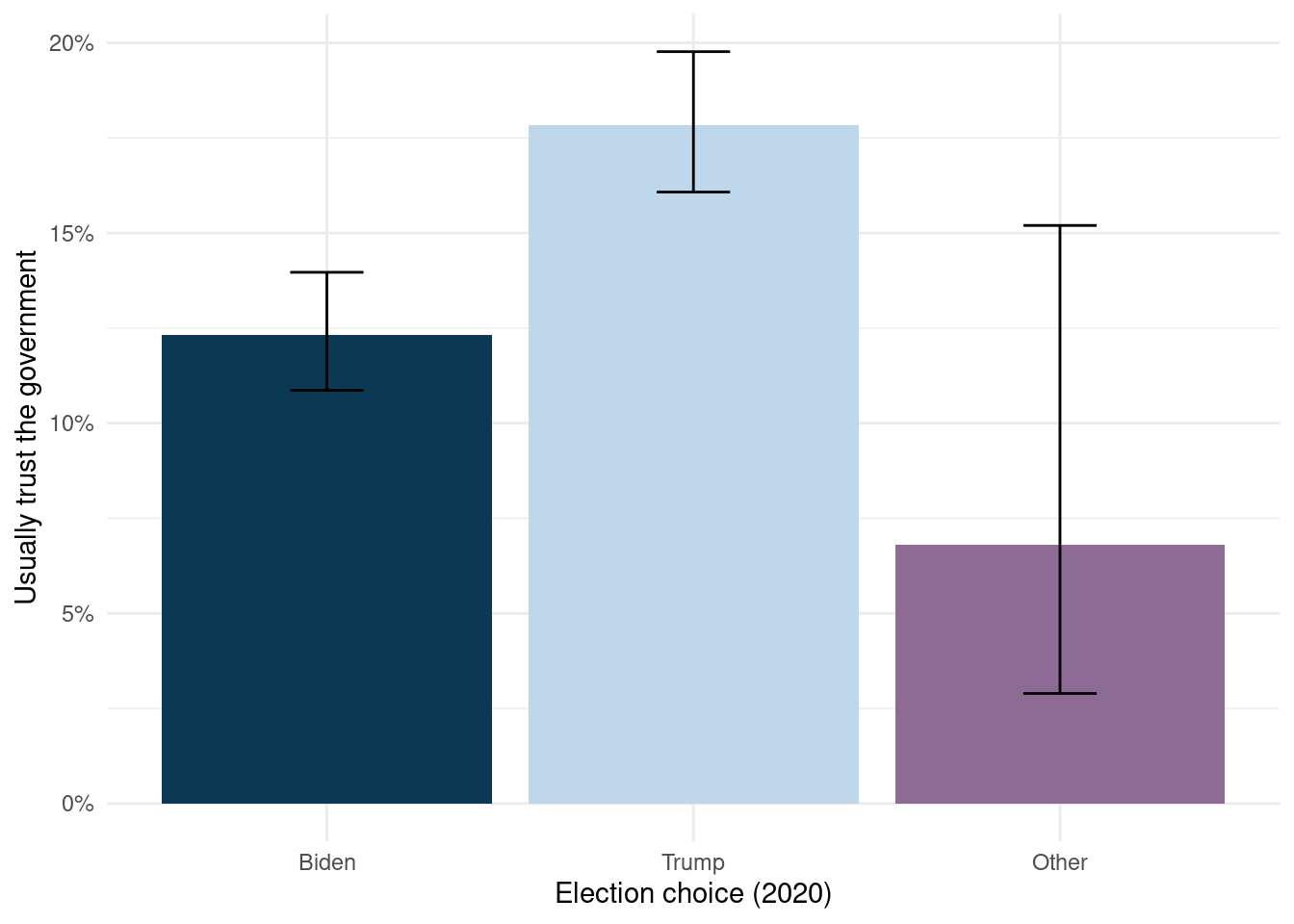

Bar chart with x-axis of election choice with levels of Biden, Trump, and Other and y-axis of 'Usually trust the government' ranging from 0% to 20%. Bar 1 is centered at 1, and length is from 0 to 0.12 with fill color dark blue which maps to VotedPres2020_selection = Biden. Bar 2 is centered at 2, and length is from 0 to 0.17 with fill color very pale blue which maps to VotedPres2020_selection = Trump. Bar 3 is centered at 3, and length is from 0 to 0.06 with fill color moderate purple which maps to VotedPres2020_selection = Other. Error bars are drawn as well with the width of the Biden and Trump error bars being similar and the error bar for Other being significantly wider.

FIGURE 7.3: Relationship between candidate selection and trust in government, ANES 2020

Looking at Figure 7.3, it appears that people who voted for Trump are more likely to say that they usually have trust in the government compared to those who voted for Biden and other candidates. To determine if this insight is accurate, we next fit the model.

logistic_trust_vote <- anes_des_der %>%
  svyglm(
    design = .,
    formula = TrustGovernmentUsually ~ VotedPres2020_selection,
    family = quasibinomial
  )

tidy(logistic_trust_vote) %>%
  mutate(p.value = pretty_p_value(p.value)) %>%
  gt() %>%
  fmt_number()

TABLE 7.6: Logistic regression output predicting trust in government by presidential candidate selection, RECS 2020
term	estimate	std.error	statistic	p.value
(Intercept)	−1.96	0.07	−27.45	<0.0001
VotedPres2020_selectionTrump	0.43	0.09	4.72	<0.0001
VotedPres2020_selectionOther	−0.65	0.44	−1.49	0.1429

In Table 7.6, we can see the estimated coefficients (estimate), estimated standard errors of the coefficients (std.error), the t-statistic (statistic), and the p-value for each coefficient. This output indicates that respondents who voted for Trump are more likely to usually have trust in the government compared to those who voted for Biden (the reference level). The coefficient of 0.435 represents the increase in the log odds of usually trusting the government.

In most cases, it is easier to talk about the odds instead of the log odds. To do this, we need to exponentiate the coefficients. We can use the same tidy() function but include the argument exponentiate = TRUE to see the odds.

tidy(logistic_trust_vote, exponentiate = TRUE) %>%
  select(term, estimate) %>%
  gt() %>%
  fmt_number()

TABLE 7.7: Logistic regression predicting trust in government by presidential candidate selection with exponentiated coefficients (odds), RECS 2020
term	estimate
(Intercept)	0.14
VotedPres2020_selectionTrump	1.54
VotedPres2020_selectionOther	0.52

Using the output in Table 7.7, we can interpret this as saying that the odds of usually trusting the government for someone who voted for Trump is 154% as likely to trust the government compared to a person who voted for Biden (the reference level). In comparison, a person who voted for neither Biden nor Trump is 52% as likely to trust the government as someone who voted for Biden.

As with linear regression, the augment() can be used to predict values. By default, the prediction is the link function, not the probability model. To predict the probability, add an argument of type.predict="response" as demonstrated below:

logistic_trust_vote %>%
  augment(type.predict = "response") %>%
  mutate(
    .se.fit = sqrt(attr(.fitted, "var")),
    .fitted = as.numeric(.fitted)
  ) %>%
  select(
    TrustGovernmentUsually,
    VotedPres2020_selection,
    .fitted,
    .se.fit
  )

## # A tibble: 6,212 × 4
##    TrustGovernmentUsually VotedPres2020_selection .fitted .se.fit
##    <lgl>                  <fct>                     <dbl>   <dbl>
##  1 FALSE                  Other                    0.0681 0.0279 
##  2 FALSE                  Biden                    0.123  0.00772
##  3 FALSE                  Biden                    0.123  0.00772
##  4 FALSE                  Trump                    0.178  0.00919
##  5 FALSE                  Biden                    0.123  0.00772
##  6 FALSE                  Trump                    0.178  0.00919
##  7 FALSE                  Biden                    0.123  0.00772
##  8 FALSE                  Biden                    0.123  0.00772
##  9 TRUE                   Biden                    0.123  0.00772
## 10 FALSE                  Biden                    0.123  0.00772
## # ℹ 6,202 more rows

Example 2: Interaction effects

Let’s look at another example with interaction effects. If we’re interested in understanding the demographics of people who voted for Biden among all voters in 2020, we could include the indicator of whether respondents voted early (EarlyVote2020) and their income group (Income7) in our model.

First, we need to subset the data to 2020 voters and then create an indicator for who voted for Biden.

anes_des_ind <- anes_des %>%
  filter(!is.na(VotedPres2020_selection)) %>%
  mutate(VoteBiden = case_when(
    VotedPres2020_selection == "Biden" ~ 1,
    TRUE ~ 0
  ))

Let’s first look at the main effects of income grouping and early voting behavior.

log_biden_main <- anes_des_ind %>%
  mutate(
    EarlyVote2020 = fct_relevel(EarlyVote2020, "No", after = 0)
  ) %>%
  svyglm(
    design = .,
    formula = VoteBiden ~ EarlyVote2020 + Income7,
    family = quasibinomial
  )

tidy(log_biden_main) %>%
  mutate(p.value = pretty_p_value(p.value)) %>%
  gt() %>%
  fmt_number()

TABLE 7.8: Logistic regression output for predicting voting for Biden given early voting behavior and income; main effects only, ANES 2020
term	estimate	std.error	statistic	p.value
(Intercept)	1.28	0.43	2.99	0.0047
EarlyVote2020Yes	0.44	0.34	1.29	0.2039
Income7$20k to < 40k	−1.06	0.49	−2.18	0.0352
Income7$40k to < 60k	−0.78	0.42	−1.86	0.0705
Income7$60k to < 80k	−1.24	0.70	−1.77	0.0842
Income7$80k to < 100k	−0.66	0.64	−1.02	0.3137
Income7$100k to < 125k	−1.02	0.54	−1.89	0.0662
Income7$125k or more	−1.25	0.44	−2.87	0.0065

This main effect model (see Table 7.8) indicates that people with incomes of $125,000 or more have a significant negative coefficient –1.25 (p-value is 0.0065). This indicates that people with incomes of $125,000 or more were less likely to vote for Biden in the 2020 election compared to people with incomes of $20,000 or less (reference level).

Although early voting behavior was not significant, there may be an interaction between income and early voting behavior. To determine this, we can create a model that includes the interaction effects:

log_biden_int <- anes_des_ind %>%
  mutate(
    EarlyVote2020 = fct_relevel(EarlyVote2020, "No", after = 0)
  ) %>%
  svyglm(
    design = .,
    formula = VoteBiden ~ (EarlyVote2020 + Income7)^2,
    family = quasibinomial
  )

tidy(log_biden_int) %>%
  mutate(p.value = pretty_p_value(p.value)) %>%
  gt() %>%
  fmt_number()

TABLE 7.9: Logistic regression output for predicting voting for Biden given early voting behavior and income; with interaction, ANES 2020
term	estimate	std.error	statistic	p.value
(Intercept)	2.32	0.67	3.45	0.0015
EarlyVote2020Yes	−0.81	0.78	−1.03	0.3081
Income7$20k to < 40k	−2.33	0.87	−2.68	0.0113
Income7$40k to < 60k	−1.67	0.89	−1.87	0.0700
Income7$60k to < 80k	−2.05	1.05	−1.96	0.0580
Income7$80k to < 100k	−3.42	1.12	−3.06	0.0043
Income7$100k to < 125k	−2.33	1.07	−2.17	0.0368
Income7$125k or more	−2.09	0.92	−2.28	0.0289
EarlyVote2020Yes:Income7$20k to < 40k	1.60	0.95	1.69	0.1006
EarlyVote2020Yes:Income7$40k to < 60k	0.99	1.00	0.99	0.3289
EarlyVote2020Yes:Income7$60k to < 80k	0.90	1.14	0.79	0.4373
EarlyVote2020Yes:Income7$80k to < 100k	3.22	1.16	2.78	0.0087
EarlyVote2020Yes:Income7$100k to < 125k	1.64	1.11	1.48	0.1492
EarlyVote2020Yes:Income7$125k or more	1.00	1.14	0.88	0.3867

The results from the interaction model (see Table 7.9) show that one interaction between early voting behavior and income is significant. To better understand what this interaction means, we can plot the predicted probabilities with an interaction plot. Let’s first obtain the predicted probabilities for each possible combination of variables using the augment() function.

log_biden_pred <- log_biden_int %>%
  augment(type.predict = "response") %>%
  mutate(
    .se.fit = sqrt(attr(.fitted, "var")),
    .fitted = as.numeric(.fitted)
  ) %>%
  select(VoteBiden, EarlyVote2020, Income7, .fitted, .se.fit)

The y-axis is the predicted probabilities, one of our x-variables is on the x-axis, and the other is represented by multiple lines. Figure 7.4 shows the interaction plot with early voting behavior on the x-axis and income represented by the lines.

log_biden_pred %>%
  filter(VoteBiden == 1) %>%
  distinct() %>%
  arrange(EarlyVote2020, Income7) %>%
  ggplot(aes(
    x = EarlyVote2020,
    y = .fitted,
    group = Income7,
    color = Income7,
    linetype = Income7
  )) +
  geom_line(linewidth = 1.1) +
  scale_color_manual(values = colorRampPalette(book_colors)(7)) +
  ylab("Predicted Probability of Voting for Biden") +
  labs(
    x = "Voted Early",
    color = "Income",
    linetype = "Income"
  ) +
  coord_cartesian(ylim = c(0, 1)) +
  guides(fill = "none") +
  theme_minimal()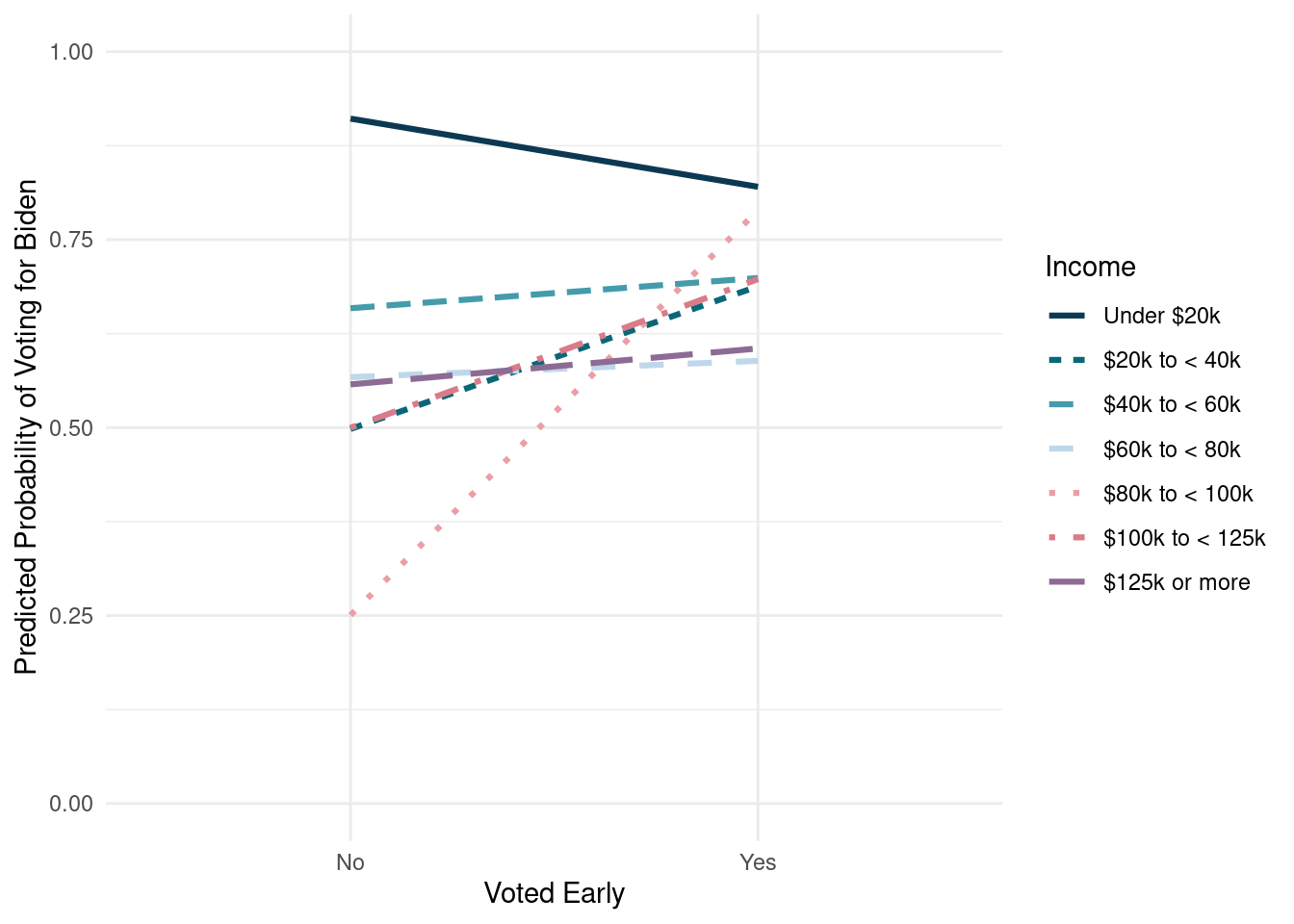

Line plot with x-axis as indicator for voted early, with did not early vote on the left and did early vote on the right, and y-axis as 'Predicted Probability of Voting for Biden'. There are seven lines for income groups with lines being from top to bottom: Under $20k, $80k to less than $100k, $40k to less than $60k, $100k to less than $125k, $20k to less than 40k, $125k or more, and $60k to less than $80k. The lines for $40k to less than $60k, $60k to less than $80k, and $125k or more are all relatively flat with the probabilities for did not early vote and did early vote being equivalent. The lines for $20k to less than $40k and $100k to less than $125k have a slight positive slope. The line for less than $20k has a slight negative slope and has overall the highest probability for both levels of early voting. The line for $80k to less than $100k has a large positive slope. This line shows the lowest probability for those who did not early vote, and the second highest probability for those who did early vote.

FIGURE 7.4: Interaction plot of early voting and income predicting the probability of voting for Biden

From Figure 7.4, we can see that people who have incomes in most groups (e.g., $40,000 to less than $60,000) have roughly the same probability of voting for Biden regardless of whether they voted early or not. However, those with income in the $100,000 to less than $125,000 group were more likely to vote for Biden if they voted early than if they did not vote early.

Interactions in models can be difficult to understand from the coefficients alone. Using these interaction plots can help others understand the nuances of the results.

7.5 Exercises

The type of housing unit may have an impact on energy expenses. Is there any relationship between housing unit type (HousingUnitType) and total energy expenditure (TOTALDOL)? First, find the average energy expenditure by housing unit type as a descriptive analysis and then do the test. The reference level in the comparison should be the housing unit type that is most common.
Does temperature play a role in electricity expenditure? Cooling degree days are a measure of how hot a place is. CDD65 for a given day indicates the number of degrees Fahrenheit warmer than 65°F (18.3°C) it is in a location. On a day that averages 65°F and below, CDD65=0, while a day that averages 85°F (29.4°C) would have CDD65=20 because it is 20 degrees Fahrenheit warmer (U.S. Energy Information Administration 2023d). Each day in the year is summed up to indicate how hot the place is throughout the year. Similarly, HDD65 indicates the days colder than 65°F. Can energy expenditure be predicted using these temperature indicators along with square footage? Is there a significant relationship? Include main effects and two-way interactions.
Continuing with our results from Exercise 2, create a plot between the actual and predicted expenditures and a residual plot for the predicted expenditures.
Early voting expanded in 2020 (Sprunt 2020). Build a logistic model predicting early voting in 2020 (EarlyVote2020) using age (Age), education (Education), and party identification (PartyID). Include two-way interactions.
Continuing from Exercise 4, predict the probability of early voting for two people. Both are 28 years old and have a graduate degree; however, one person is a strong Democrat, and the other is a strong Republican.

References

American National Election Studies. 2021. “ANES 2020 Time Series Study: Pre-Election and Post-Election Survey Questionnaires.” https://electionstudies.org/wp-content/uploads/2021/07/anes_timeseries_2020_questionnaire_20210719.pdf.

Bollen, Kenneth A., Paul P. Biemer, Alan F. Karr, Stephen Tueller, and Marcus E. Berzofsky. 2016. “Are Survey Weights Needed? A Review of Diagnostic Tests in Regression Analysis.” Annual Review of Statistics and Its Application 3 (1): 375–92. https://doi.org/10.1146/annurev-statistics-011516-012958.

Gelman, Andrew. 2007. “Struggles with Survey Weighting and Regression Modeling.” Statistical Science 22 (2): 153–64. https://doi.org/10.1214/088342306000000691.

Iannone, Richard, Joe Cheng, Barret Schloerke, Ellis Hughes, Alexandra Lauer, JooYoung Seo, Ken Brevoort, and Olivier Roy. 2024. gt: Easily Create Presentation-Ready Display Tables. https://github.com/rstudio/gt.

Lumley, Thomas. 2010. Complex Surveys: A Guide to Analysis Using R. John Wiley & Sons.

McCullagh, Peter, and John Ashworth Nelder. 1989. “Binary Data.” In Generalized Linear Models, 98–148. Springer.

R Core Team. 2024. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Robinson, David, Alex Hayes, and Simon Couch. 2023. broom: Convert Statistical Objects into Tidy Tibbles. https://broom.tidymodels.org/.

Sprunt, Barbara. 2020. “93 Million and Counting: Americans Are Shattering Early Voting Records.” National Public Radio.

———. 2020. “Residential Energy Consumption Survey (RECS) Form EIA-457A 2020 Household Questionnaire.” https://www.eia.gov/survey/form/eia_457/archive/2020_RECS-457A.pdf.

———. 2023d. “Units and Calculators Explained: Degree Days.” https://www.eia.gov/energyexplained/units-and-calculators/degree-days.php.

Use help(formula) or ?formula in R↩︎
There is some debate about whether weights should be used in regression (Bollen et al. 2016; Gelman 2007). However, for the purposes of providing complete information on how to analyze complex survey data, this chapter includes weights.↩︎
Question text: “During the summer, what is your home’s typical indoor temperature inside your home at night?” (U.S. Energy Information Administration 2020)↩︎
Question text: “Is any air conditioning equipment used in your home?” (U.S. Energy Information Administration 2020)↩︎
Question text: “What is the square footage of your home?” (U.S. Energy Information Administration 2020)↩︎
Question text: “How often can you trust the federal government in Washington to do what is right?” (American National Election Studies 2021)↩︎